题目内容
满足arccos(x2)>arccos(2x)的实数x的取值范围是 .
考点:三角不等式
专题:三角函数的图像与性质
分析:由arccos(x2)>arccos(2x),可得0≤x2<2x≤1,解出即可.
解答:
解:∵arccos(x2)>arccos(2x),
∴0≤x2<2x≤1,
解得0<x≤
.
故答案为:(0,
].
∴0≤x2<2x≤1,
解得0<x≤
| 1 |
| 2 |
故答案为:(0,
| 1 |
| 2 |
点评:本题考查了反三角函数的单调性,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
若关于x的方程
=m-x有两个不等的实根,则m的取值范围是( )
| -x2-2x |
A、(-
| ||||
B、(-2,
| ||||
C、(0,
| ||||
D、[0,
|
使不等式23x-1>1成立的x的取值为( )
A、(
| ||
| B、(1,+∞) | ||
C、(
| ||
D、(-
|
若tanx=2则cos2x=( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知a=log
3,b=log
2,c=20.3,则a,b,c三者的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、c>b>a |
| B、a>c>b |
| C、b>a>c |
| D、c>a>b |
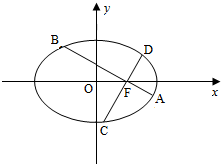 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆