题目内容
18．设关于x的方程x2-ax-1=0和x2-x-2a=0的实根分别为x1、x2和x3、x4，若x1＜x3＜x2＜x4，则实数a的取值范围为$（0，\frac{3-\sqrt{3}}{2}）$．分析 由x2-ax-1=0得ax=x2-1，由x2-x-2a=0得2a=x2-x，构造函数y=x2-x和y=2x-$\frac{2}{x}$，在同一坐标系中作出两个函数得图象，并求出x2-x=2x-$\frac{2}{x}$的解即两图象交点的横坐标，结合条件和函数的图象求出a的取值范围．
解答 解：由x2-x-2a=0得2a=x2-x，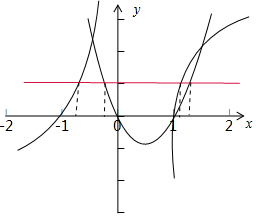
由x2-ax-1=0（x≠0）得ax=x2-1，则2a=2x-$\frac{2}{x}$，
作出函数y=x2-x和y=2x-$\frac{2}{x}$的函数图象如下图：
由x2-x=2x-$\frac{2}{x}$得，x2-3x+$\frac{2}{x}$=0，则$\frac{{x}^{3}-3{x}^{2}+2}{x}$=0，
∴$\frac{{（x-1）（x}^{2}-2x-2）}{x}$=0，
解得x=1或x=1$+\sqrt{3}$或x=$1-\sqrt{3}$，
∵x1＜x3＜x2＜x4，且当x=$1-\sqrt{3}$时，可得a=$\frac{3-\sqrt{3}}{2}$，
∴由图可得，0＜a＜$\frac{3-\sqrt{3}}{2}$，
故答案为：$（0，\frac{3-\sqrt{3}}{2}）$．
点评 本题考查方程的根、函数的零点与函数图象交点之间的转化，以及构造函数法、数形结合思想，属于难题．
练习册系列答案
相关题目
8．已知函数f（x）=x2-cosx，对于$[-\frac{π}{2}，\frac{π}{2}]$上的任意x1，x2，有如下条件：①x1＞x2；②$x_1^2＞x_2^2$；③|x1|＞x2，其中能使f（x）1＞f（x2）恒成立的条件序号是（ ）
| A． | ① | B． | ② | C． | ③ | D． | 以上都不对 |
8．将函数f（x）=cos2x（x∈R）的图象沿向量$\overrightarrow{a}$平移后，所得曲线对应的函数在区间[$\frac{π}{3}$，$\frac{2π}{3}$]内单调递增，且在该区间的最大值为1，则向量$\overrightarrow{a}$可能是（ ）
| A． | （-$\frac{π}{6}$，$\frac{1}{2}$） | B． | （$\frac{π}{6}$，$\frac{1}{2}$） | C． | （$\frac{π}{3}$，$\frac{3}{2}$） | D． | （-$\frac{π}{3}$，$\frac{3}{2}$） |