题目内容
已知圆 的圆心在直线
的圆心在直线 上,且与
上,且与 轴交于两点
轴交于两点 ,
, .
.
(1)求圆 的方程;
的方程;
(2)求过点
 的圆
的圆 的切线方程.
的切线方程.
(1)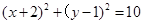 ;(2)
;(2)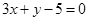 .
.
解析试题分析:(1)先联立直线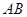 的中垂线方程与直线方程
的中垂线方程与直线方程 ,求出交点的坐标即圆心
,求出交点的坐标即圆心 的坐标,然后再计算出
的坐标,然后再计算出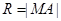 ,最后就可写出圆
,最后就可写出圆 的标准方程;(2)求过点的圆的切线方程问题,先判断点
的标准方程;(2)求过点的圆的切线方程问题,先判断点 在圆
在圆 上还是在圆
上还是在圆 外,若点
外,若点 在圆
在圆 上,则所求直线的斜率为
上,则所求直线的斜率为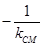 ,由点斜式即可写出切线的方程,若点
,由点斜式即可写出切线的方程,若点 在圆
在圆 外,则可设切线方程为
外,则可设切线方程为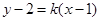 (此时注意验证斜率不存在的情形),然后由圆心
(此时注意验证斜率不存在的情形),然后由圆心 到切线的距离等于半径,求出
到切线的距离等于半径,求出 即可求出切线的方程.
即可求出切线的方程.
试题解析:(1)因为圆 与
与 轴交于两点
轴交于两点 ,
, ,所以圆心在直线
,所以圆心在直线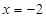 上
上
由 得
得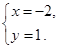 即圆心
即圆心 的坐标为
的坐标为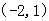 2分
2分
半径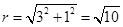
所以圆 的方程为
的方程为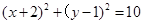 4分
4分
(2)由 坐标可知点
坐标可知点 在圆
在圆 上,由
上,由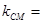
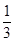 ,可知切线的斜率为
,可知切线的斜率为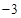 6分
6分
故过点
 的圆
的圆 的切线方程为
的切线方程为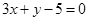 8分.
8分.
考点:1.圆的方程;2.直线与圆的位置关系.

练习册系列答案
相关题目

 (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点. 经过坐标原点
经过坐标原点 和点
和点 ,且圆心在
,且圆心在 轴上.
轴上. 经过点
经过点 ,且
,且 ,求直线
,求直线 .
. 相交于M,N两点,且
相交于M,N两点,且 (
(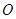 为坐标原点)求
为坐标原点)求 的值;
的值; 为直径的圆的方程.
为直径的圆的方程. 与圆
与圆 外切于点
外切于点 ,直线
,直线 是两圆的外公切线,分别与两圆相切于
是两圆的外公切线,分别与两圆相切于 两点,
两点, 是圆
是圆 作圆
作圆 .
.
 三点共线;
三点共线; .
. 轴截得的弦长为
轴截得的弦长为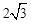 ,圆C的面积小于13.
,圆C的面积小于13.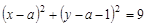 ,其中
,其中 为实常数.
为实常数. 被圆C截得的弦长为2,求
被圆C截得的弦长为2,求 ,0为坐标原点,若圆C上存在点M,使|MA|="2" |MO|,求
,0为坐标原点,若圆C上存在点M,使|MA|="2" |MO|,求 的取值范围.
的取值范围.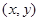 到定点
到定点 与到定点
与到定点 的距离之比为3.
的距离之比为3. ,若曲线C上恰有两个点到直线
,若曲线C上恰有两个点到直线 的距离为1,
的距离为1, 的取值范围。
的取值范围。