题目内容
如图,已知椭圆C:| x2 |
| 5 |
| y2 |
| 3 |
| m2 |
| 2 |
(1)是否存在k,使对任意m>0,总有
| OA |
| OB |
| ON |
(2)若
| OA |
| OB |
| 1 |
| 2 |
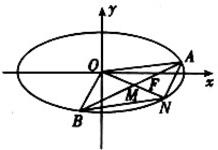
分析:(1)椭圆C:
+
=1,c2=
-
=m2,c=m,F(m,0),直线AB:y=k(x-m),由
,得(10k2+6)x2-20k2mx+10k2m2-15m2=0.设A(x1,y1),B(x2,y2),然后结合韦达定理进行求解.
(2)
•
=x1x2+y1y2=x1x2+k2(x1-m)(x2-m)=(1+k2)x1x2-k2m(x1+x2)+k2m2=(1+k2)•由此结合
•
=-
(m3+4m),能够导出实数k的取值范围.
| x2 | ||
|
| y2 | ||
|
| 5m2 |
| 2 |
| 3m2 |
| 2 |
|
(2)
| OA |
| OB |
| OA |
| OB |
| 1 |
| 2 |
解答:解:(1)椭圆C:
+
=1,c2=
-
=m2,c=m,∴F(m,0),直线AB:y=k(x-m),
,(10k2+6)x2-20k2mx+10k2m2-15m2=0.设A(x1,y1),B(x2,y2),
则x1+x2=
,
x1x2=
;则xm=
=
,ym=k(xm-m)=
,
若存在k,使AB为ON的中点,∴
+
=2
.
∴
+
=(2xm,2ym)=(
,
),
即N点坐标为(
,
).由N点在椭圆上,
则
×(
)2+
×(
)2=
即5k4-2k2-3=0.∴k2=1或k2=-
(舍).故存在k=±1使
+
=
.
(2)
•
=x1x2+y1y2=x1x2+k2(x1-m)(x2-m)
=(1+k2)x1x2-k2m(x1+x2)+k2m2
=(1+k2)•
-k2m•
+k2m2=
m2,
由m2•
=-
(m3+4m),得m2•
=-
(m+
)≤-2m2,
即k2-15≤-20k2-12,k2≤
,∴-
≤k≤
,且k≠0.
| x2 | ||
|
| y2 | ||
|
| 5m2 |
| 2 |
| 3m2 |
| 2 |
|
则x1+x2=
| 20k2m |
| 10k2+6 |
x1x2=
| 10k2m2-15m2 |
| 10k2+6 |
| x1+x2 |
| 2 |
| 10k2m |
| 10k2+6 |
| -6km |
| 10k2+6 |
若存在k,使AB为ON的中点,∴
| OA |
| OB |
| OM |
∴
| OA |
| OB |
| 20k2m |
| 10k2+6 |
| -12km |
| 10k2+6 |
即N点坐标为(
| 20k2m |
| 10k2+6 |
| -12km |
| 10k2+6 |
则
| 1 |
| 5 |
| 20k2m |
| 10k2+6 |
| 1 |
| 3 |
| -12km |
| 10k2+6 |
| m2 |
| 2 |
即5k4-2k2-3=0.∴k2=1或k2=-
| 3 |
| 5 |
| OA |
| OB |
| ON |
(2)
| OA |
| OB |
=(1+k2)x1x2-k2m(x1+x2)+k2m2
=(1+k2)•
| 10k2m2-15m2 |
| 10k2+6 |
| 20k2m |
| 10k2+6 |
| (k2-15) |
| 10k2+6 |
由m2•
| (k2-15) |
| 10k2+6 |
| 1 |
| 2 |
| k2-15 |
| 10k2+6 |
| m2 |
| 2 |
| 4 |
| m |
即k2-15≤-20k2-12,k2≤
| 1 |
| 7 |
| ||
| 7 |
| ||
| 7 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆C:
如图,已知椭圆C: (2012•深圳一模)如图,已知椭圆C:
(2012•深圳一模)如图,已知椭圆C: 如图,已知椭圆
如图,已知椭圆