题目内容
已知等差数列{an}的首项为a1,公差为d,其前n项和为Sn,若直线y=
a1x+m与圆(x-2)2+y2=1的两个交点关于直线x+y-d=0对称,则数列{
}的前10项和=( )
| 1 |
| 2 |
| 1 |
| Sn |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:利用直线y=
a1x+m与圆(x-2)2+y2=1的两个交点关于直线x+y-d=0对称,可得a1=2,d=2,利用等差数列的求和公式求出Sn,再用裂项法即可得到结论.
| 1 |
| 2 |
解答:解:∵直线y=
a1x+m与圆(x-2)2+y2=1的两个交点关于直线x+y-d=0对称,
∴a1=2,2-d=0
∴d=2
∴Sn=2n+
×2=n2+n
∴
=
-
,
∴数列{
}的前10项和为1-
+
-
+…+
-
=
故选:B.
| 1 |
| 2 |
∴a1=2,2-d=0
∴d=2
∴Sn=2n+
| n(n-1) |
| 2 |
∴
| 1 |
| Sn |
| 1 |
| n |
| 1 |
| n+1 |
∴数列{
| 1 |
| Sn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 10 |
| 1 |
| 11 |
| 10 |
| 11 |
故选:B.
点评:本题考查直线与圆的位置关系,考查圆的对称性,考查等差数列的求和公式,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学共有学生2000名,抽取了一个容量为200的样本,已知样本中女生比男生少6人,则该校共有女生( )
| A、1030人 | B、97人 | C、950人 | D、970人 |
当x∈[-
,
]时,函数f(x)=sinx+
cosx的最大值与最小值分别是( )
| π |
| 2 |
| π |
| 2 |
| 3 |
| A、1,-1 | ||
B、1,-
| ||
| C、2,-2 | ||
| D、2,-1 |
在△ABC中,A-B=
,sinC=
,AB=
,则AC=( )
| π |
| 2 |
| 1 |
| 3 |
| 3 |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、3
|
若{bn}为等差数列,b2=4,b4=8.数列{an}满足a1=1,bn=an+1-an(n∈N*),则a8=( )
| A、56 | B、57 | C、72 | D、73 |
《张邱建算经》有一道题:今有女子不善织布,逐日所织的布同数递减,初日织五尺,末一日织一尺,计织三十日,问共织布( )
| A、110尺 | B、90尺 | C、60尺 | D、30尺 |
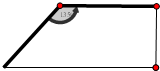 两直立矮墙成135°二面角,现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园(墙足够长),则所用篱笆总长度的最小值为( )
两直立矮墙成135°二面角,现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园(墙足够长),则所用篱笆总长度的最小值为( )| A、16m | ||
| B、18m | ||
| C、22.5m | ||
D、15
|
若p:φ=
+kπ,k∈Z,q:f(x)=sin(ωx+φ)(ω≠0)是偶函数,则p是q的( )
| π |
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |