题目内容
【题目】已知关于
的一元二次方程
.
（1）若
，
，求方程有实根的概率；
（2）若
，
，求方程有实根的概率.
【答案】(1) 
(2) 
【解析】
首先确定要使方程有实根，需判别式
，即
；（1）列出
所有可能的取值，找出其中的个数，根据古典概型求得结果；（2）在平面直角坐标系中画出所有可能取值构成的区域；再画出满足的所有区域；利用几何概型求得结果.
用表示
取相应值时所对应的一个一元二次方程
要使
有实根，则，即
（1）的所有可能取值有
个：
，
，
，
，
，
，
，
，
，
，
，
其中满足的有
个
故方程有实根的概率为：
（2）设事件
表示“一元二次方程有实根”
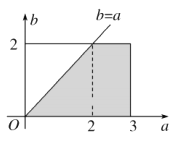
的所有可能取值构成的区域为
，这是一个长方形区域，面积为
；
构成事件的区域为
，如图中阴影部分，面积为
故方程有实根的概率为：
练习册系列答案
相关题目
【题目】某舆情机构为了解人们对某事件的关注度，随机抽取了
人进行调查，其中女性中对该事件关注的占
，而男性有
人表示对该事件没有关注.
关注 | 没关注 | 合计 | |
男 |
| ||
女 | |||
合计 |
（1）根据以上数据补全
列联表；
（2）能否有
的把握认为“对事件是否关注与性别有关”？
（3）已知在被调查的女性中有名大学生，这其中有
名对此事关注.现在从这名女大学生中随机抽取
人，求至少有
人对此事关注的概率.
附表：
|
|
|
|
|
|
|
|
|
|
|
|
