题目内容
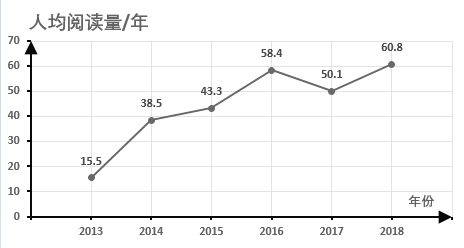
【题目】一个多面体的直观图及三视图如图所示，其中M ，N 分别是AF、BC 的中点
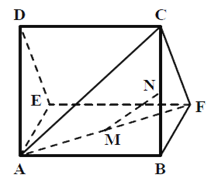
（1）求证：MN∥平面CDEF；
（2）求多面体A-CDEF的体积．
【答案】（1）详见解析；（2）
．
【解析】
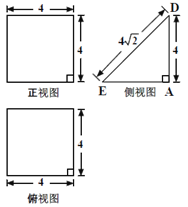
由三视图可知，该多面体是底面为直角三角形的直三棱柱ADE-BCF，且底面是一个直角三角形，由三视图中所标数据易计算出三棱柱中各棱长的值．
（1）取BF的中点G，连接MG、NG，利用中位线的性质结合线面平行的充要条件，易证明结论
（2）多面体A-CDEF的体积是一个四棱锥，由三视图易求出棱锥的底面面积和高，进而得到棱锥的体积．
（1）证明：由三视图知，该多面体是底面为直角三角形的直三棱柱ADE-BCF，且AB=BC=BF=4，DE=CF=
，
，连结BE，M在BE上，连结CE
EM=BM，CN=BN，所以
∥
，所以
平面
（2）取DE的中点H．
∵AD=AE，∴AH⊥DE，
在直三棱柱ADE-BCF中，
平面ADE⊥平面CDEF，
平面ADE∩平面CDEF=DE．∴AH⊥平面CDEF．
∴多面体A-CDEF是以AH为高，以矩形CDEF为底面的棱锥，在△ADE中，AH=
．
S矩形CDEF=DEEF=，
∴棱锥A-CDEF的体积为
．
名校课堂系列答案【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售．如果当天卖不完，剩下的玫瑰花做垃圾处理．
（Ⅰ）若花店一天购进17枝玫瑰花，求当天的利润y(单位：元)关于当天需求量n（单位：枝，n∈N）的函数解析式．
（Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(i)假设花店在这100天内每天购进17枝玫瑰花，求这100天的日利润（单位：元）的平均数；
(ii)若花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率.
（命题意图）本题主要考查给出样本频数分别表求样本的均值、将频率做概率求互斥事件的和概率，是简单题.
