题目内容
已知数列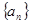 是等差数列,
是等差数列,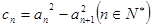
(1)判断数列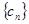 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)如果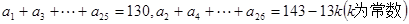 ,试写出数列
,试写出数列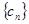 的通项公式;
的通项公式;
(3)在(2)的条件下,若数列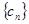 得前n项和为
得前n项和为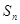 ,问是否存在这样的实数
,问是否存在这样的实数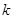 ,使
,使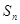 当且仅当
当且仅当 时取得最大值。若存在,求出
时取得最大值。若存在,求出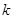 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(1)数列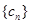 是以
是以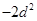 为公差的等差数列.(2)
为公差的等差数列.(2)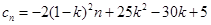 .
.
(3)存在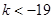 或
或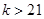 .
.
解析试题分析:1)设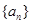 的公差为
的公差为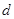 ,确定
,确定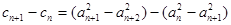
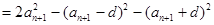
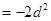 ,作出结论.
,作出结论.
(2)根据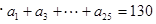 ,
,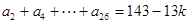 ,
,
建立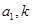 的方程组,首先求得
的方程组,首先求得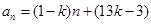
进一步确定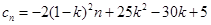 .
.
(3)由已知当且仅当 时
时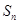 最大,
最大,
得到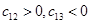 ,建立
,建立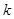 的不等式组,求得
的不等式组,求得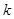 的范围.
的范围.
试题解析:(1)设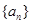 的公差为
的公差为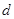 ,则
,则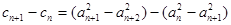
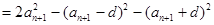
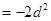
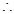 数列
数列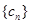 是以
是以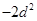 为公差的等差数列 3
为公差的等差数列 3
(2)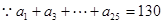
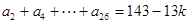
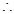 两式相减:
两式相减:
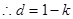 6分
6分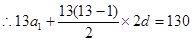
 8分
8分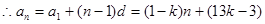
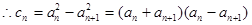
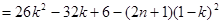
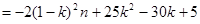 8
8
(3)因为当且仅当 时
时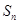 最大,
最大,
有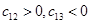
即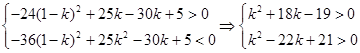
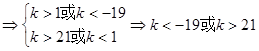 12
12
考点:等差数列,一元二次不等式组的解法.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
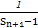 ,其前n项和为Tn,求证:Tn<
,其前n项和为Tn,求证:Tn< (n∈N*).
(n∈N*).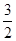 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列. (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.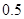 万人,从2023年开始到2032年每年人口为上一年的99%.
万人,从2023年开始到2032年每年人口为上一年的99%. 年的人口总数
年的人口总数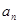 的表达式(注:2013年为第一年);
的表达式(注:2013年为第一年);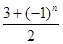 ,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n, .
.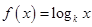 (
(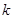 为常数,
为常数,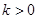 且
且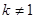 ),且数列
),且数列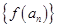 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。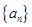 是等比数列;
是等比数列;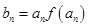 ,当
,当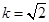 时,求数列
时,求数列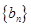 的前n项和
的前n项和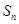 。
。