题目内容
数列{an}中，a1＝8，a4＝2，且满足：an+2－2an+1＋an＝0（n∈N*），
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设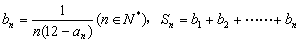
，是否存在最大的整数m，使得任意的n均有
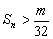总成立？若存在，求出m；若不存在，请说明理由．
【答案】
（Ⅰ）∵an+an+1＋an＝0，∴an+2－an+1＝an+1－an（n∈N*），
∴{an}是等差数列，设公差为d，
∵a1＝8，a4＝a1＋3d＝8＋3d＝2，∴d＝－2，
∴an＝8＋（n－1）·（－2）＝n．
（Ⅱ）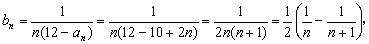
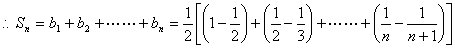
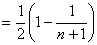
假设存在整数m满足
总成立，
又
∴数列{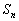
}是单调递增的，
∴
为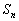的最小值，故
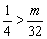，即m＜8，又m∈N*，
∴适当条件的m的最大值为7．
练习册系列答案
字词句段篇系列答案
相关题目
数列{an}中，a1=
，an+an+1=
，n∈N*，则
（a1+a2+…+an）等于（ ）
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|