题目内容
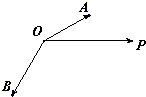如图，已知单位向量| OA |
| OB |
| OP |
为
| π |
| 6 |
| 2π |
| 3 |
| DC |
| OA |
| OB |
| DC |
| OP |
分析：根据两个向量之差是一个向量，可以看出这三个向量组成顶角是150°的三角形，单位向量
、
与向量
共面根据三角形内角之间的关系，和向量的减法运算，得到要求的角的度数．
| OA |
| OB |
| OP |
解答：解：∵
=
-
，
单位向量
、
与向量
共面，且夹角分别为
和
，
∴
，
，
组成夹角是150°的等腰三角形，
∴向量
与
的夹角是180°-120°-15°=45°，
故答案为：45°
| OC |
| OA |
| OB |
单位向量
| OA |
| OB |
| OP |
| π |
| 6 |
| 2π |
| 3 |
∴
| OA |
| OB |
| DC |
∴向量
| DC |
| OP |
故答案为：45°
点评：本题考查向量的加减运算，是一个基础题，向量的加减运算是用向量解决问题的基础，要学好运算，才能用向量解决立体几何问题，三角函数问题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
（2012•九江一模）已知点G是△ABC的外心，
选修4-2：矩阵及其变换
[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
附加题：（选做题：在下面A、B、C、D四个小题中只能选做两题）
，求线段AC的长度．
和特征值λ2=2及对应的一个特征向量
，试求矩阵A．
（θ是参数），若以O为极点，x轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线C的极坐标方程．