题目内容
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)A.选修4-1:几何证明选讲
如图,已知AB、CD是圆O的两条弦,且AB是线段CD的垂直平分线,
已知AB=6,CD=2
 ,求线段AC的长度.
,求线段AC的长度.B.选修4-2:矩阵与变换
已知二阶矩阵A有特征值λ1=1及对应的一个特征向量
 和特征值λ2=2及对应的一个特征向量
和特征值λ2=2及对应的一个特征向量 ,试求矩阵A.
,试求矩阵A.C.选修4-4:坐标系与参数方程
在直角坐标系xOy中,已知曲线C的参数方程是
 (θ是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(θ是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.D.选修4-5:不等式选讲
已知关于x的不等式|ax-1|+|ax-a|≥1(a>0).
(1)当a=1时,求此不等式的解集;
(2)若此不等式的解集为R,求实数a的取值范围.

【答案】分析:A.连接BC,设AB,CD相交于点E,AE=x,由AB是线段CD的垂直平分线,知AB是圆的直径,∠ACB=90°,则EB=6-x,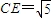 .由射影定理得x(6-x)=5,由此能求出线段落AC的长度.
.由射影定理得x(6-x)=5,由此能求出线段落AC的长度.
B.设矩阵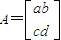 ,这里a,b,c,d∈R,因为
,这里a,b,c,d∈R,因为 是矩阵A的属于λ1=1的特征向量,所以
是矩阵A的属于λ1=1的特征向量,所以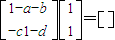 ,因为
,因为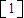 是矩阵A的属于λ2=2的特征向量,所以
是矩阵A的属于λ2=2的特征向量,所以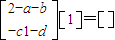 ,由此能求出矩阵A.
,由此能求出矩阵A.
C.由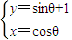 得
得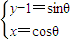 ,两式平方后相加得x2+(y-1)2=1,所以曲线C是以(0,1)为圆心,半径等于1的圆.由此能求出曲线C的极坐标方程.
,两式平方后相加得x2+(y-1)2=1,所以曲线C是以(0,1)为圆心,半径等于1的圆.由此能求出曲线C的极坐标方程.
D.(1)当a=1时,得2|x-1|≥1,由此能求出不等式的解集.
(2)由|ax-1|+|ax-a|≥|a-1|,知原不等式解集为R等价于|a-1|≥1.由此能求出实数a的取值范围.
解答: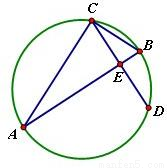 解:A.(选修4-l:几何证明选讲)
解:A.(选修4-l:几何证明选讲)
连接BC设AB,CD相交于点E,AE=x,
∵AB是线段CD的垂直平分线,
∴AB是圆的直径,∠ACB=90°(2分)
则EB=6-x,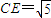 .由射影定理得CE2=AE•EB,
.由射影定理得CE2=AE•EB,
即有x(6-x)=5,解得x=1(舍)或x=5(8分)
∴AC2=AE•AB=5×6=30,即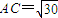 .(10分)
.(10分)
B.(选修4-2:矩阵与变换)
设矩阵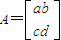 ,这里a,b,c,d∈R,
,这里a,b,c,d∈R,
因为 是矩阵A的属于λ1=1的特征向量,
是矩阵A的属于λ1=1的特征向量,
则有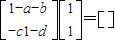 ①,(4分)
①,(4分)
又因为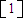 是矩阵A的属于λ2=2的特征向量,
是矩阵A的属于λ2=2的特征向量,
则有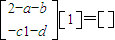 ②,(6分)
②,(6分)
根据①②,则有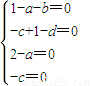 (8分)
(8分)
从而a=2,b=-1,c=0,d=1,
因此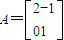 ,(10分)
,(10分)
C.(选修4-4:坐标系与参数方程)
由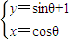 得
得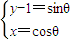 ,
,
两式平方后相加得x2+(y-1)2=1,(4分)
∴曲线C是以(0,1)为圆心,半径等于1的圆
令x=ρcosθ,y=ρsinθ,
代入并整理得ρ=2sinθ.即曲线C的极坐标方程是ρ=2sinθ. (10分)
D.(选修4-5:不等式选讲)
(1)当a=1时,得2|x-1|≥1,即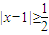 ,
,
解得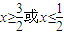 ,
,
∴不等式的解集为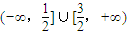 . (5分)
. (5分)
(2)∵|ax-1|+|ax-a|≥|a-1|,
∴原不等式解集为R等价于|a-1|≥1.
∴a-1≥1,或a-1≤-1.
∴a≥2,或a≤0.
∵a>0,∴a≥2.∴实数a的取值范围为[2,+∞). (10分)
点评:A.本题考查线段长度的求法,是基础题,解题时要认真审题,注意圆的性质的灵活运用.
B.本题考查矩阵与变换的应用,是基础题,解题时要认真审题,注意特征方程和特征值的合理运用.
C.本题考查参数方程和极坐标方程的应用,是基础题.解题时要认真审题,注意把极坐标方程恰当地转化为普通方程.
D.本题考查不等式的解法和求实数a的取值范围.解题时要认真审题,仔细解答,注意含绝对值不等式性质的合理运用.
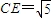 .由射影定理得x(6-x)=5,由此能求出线段落AC的长度.
.由射影定理得x(6-x)=5,由此能求出线段落AC的长度.B.设矩阵
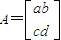 ,这里a,b,c,d∈R,因为
,这里a,b,c,d∈R,因为 是矩阵A的属于λ1=1的特征向量,所以
是矩阵A的属于λ1=1的特征向量,所以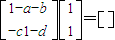 ,因为
,因为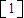 是矩阵A的属于λ2=2的特征向量,所以
是矩阵A的属于λ2=2的特征向量,所以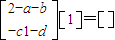 ,由此能求出矩阵A.
,由此能求出矩阵A.C.由
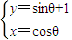 得
得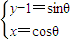 ,两式平方后相加得x2+(y-1)2=1,所以曲线C是以(0,1)为圆心,半径等于1的圆.由此能求出曲线C的极坐标方程.
,两式平方后相加得x2+(y-1)2=1,所以曲线C是以(0,1)为圆心,半径等于1的圆.由此能求出曲线C的极坐标方程.D.(1)当a=1时,得2|x-1|≥1,由此能求出不等式的解集.
(2)由|ax-1|+|ax-a|≥|a-1|,知原不等式解集为R等价于|a-1|≥1.由此能求出实数a的取值范围.
解答:
 解:A.(选修4-l:几何证明选讲)
解:A.(选修4-l:几何证明选讲)连接BC设AB,CD相交于点E,AE=x,
∵AB是线段CD的垂直平分线,
∴AB是圆的直径,∠ACB=90°(2分)
则EB=6-x,
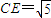 .由射影定理得CE2=AE•EB,
.由射影定理得CE2=AE•EB,即有x(6-x)=5,解得x=1(舍)或x=5(8分)
∴AC2=AE•AB=5×6=30,即
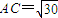 .(10分)
.(10分)B.(选修4-2:矩阵与变换)
设矩阵
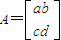 ,这里a,b,c,d∈R,
,这里a,b,c,d∈R,因为
 是矩阵A的属于λ1=1的特征向量,
是矩阵A的属于λ1=1的特征向量,则有
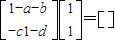 ①,(4分)
①,(4分)又因为
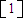 是矩阵A的属于λ2=2的特征向量,
是矩阵A的属于λ2=2的特征向量,则有
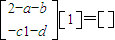 ②,(6分)
②,(6分)根据①②,则有
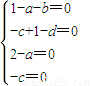 (8分)
(8分)从而a=2,b=-1,c=0,d=1,
因此
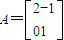 ,(10分)
,(10分)C.(选修4-4:坐标系与参数方程)
由
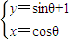 得
得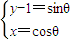 ,
,两式平方后相加得x2+(y-1)2=1,(4分)
∴曲线C是以(0,1)为圆心,半径等于1的圆
令x=ρcosθ,y=ρsinθ,
代入并整理得ρ=2sinθ.即曲线C的极坐标方程是ρ=2sinθ. (10分)
D.(选修4-5:不等式选讲)
(1)当a=1时,得2|x-1|≥1,即
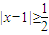 ,
,解得
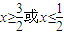 ,
,∴不等式的解集为
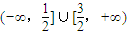 . (5分)
. (5分)(2)∵|ax-1|+|ax-a|≥|a-1|,
∴原不等式解集为R等价于|a-1|≥1.
∴a-1≥1,或a-1≤-1.
∴a≥2,或a≤0.
∵a>0,∴a≥2.∴实数a的取值范围为[2,+∞). (10分)
点评:A.本题考查线段长度的求法,是基础题,解题时要认真审题,注意圆的性质的灵活运用.
B.本题考查矩阵与变换的应用,是基础题,解题时要认真审题,注意特征方程和特征值的合理运用.
C.本题考查参数方程和极坐标方程的应用,是基础题.解题时要认真审题,注意把极坐标方程恰当地转化为普通方程.
D.本题考查不等式的解法和求实数a的取值范围.解题时要认真审题,仔细解答,注意含绝对值不等式性质的合理运用.

练习册系列答案
相关题目
 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题) -
- 在闭区间
在闭区间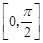 上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.