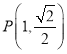题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)当![]() 时,是否存在正实数
时,是否存在正实数![]() ,当
,当![]() (
(![]() 是自然对数底数)时,函数
是自然对数底数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
【答案】(1)最大值是![]() ,最小值为
,最小值为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)先求出导函数![]() ,在求出
,在求出![]() 的单调区间,进而求得极大值与极小值,比较端点值可得最大值与最小值;(2)当
的单调区间,进而求得极大值与极小值,比较端点值可得最大值与最小值;(2)当![]() 时,分三种情况讨论函数的单调性,进而求出函数
时,分三种情况讨论函数的单调性,进而求出函数![]() 的最小值(用
的最小值(用![]() 表示),令其等于
表示),令其等于![]() 即可求出
即可求出![]() 的值.
的值.
试题解析: (1)当![]() 时,
时,![]() ,且
,且![]() ,
,
![]() .
.
得![]() 时
时![]() ;
;![]() 时
时![]() ,
,
所以函数![]() 在
在![]() 上单调递增;,函数
上单调递增;,函数![]() 在
在![]() 上单调递减,
上单调递减,
所以函数![]() 在区间
在区间![]() 仅有极大值点
仅有极大值点![]() ,故这个极大值点也是最大值点,
,故这个极大值点也是最大值点,
故函数在![]() 最大值是
最大值是![]() ,
,
又![]() ,故
,故![]() ,
,
故函数在![]() 上的最小值为
上的最小值为![]() .
.
(2)
(ⅰ)![]()
(ⅱ)![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
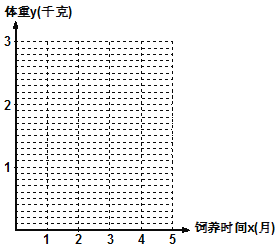
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.
(2)请根据上表提供的数据,用最小二乘法求出变量![]() 关于变量
关于变量![]() 的线性回归直线方程
的线性回归直线方程![]() .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: 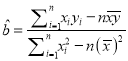 ,
, ![]() )
)
【题目】英州市育才中学对全体教师在教学中是否经常使用信息技术实施教学的情况进行了调查得到统计数据如下(表)
教师教龄 |
|
|
|
|
教师人数 |
|
|
|
|
经常使用信息技术实施教学的人数 |
|
|
|
|
(1)求该校教师在教学中不经常使用信息技术实施教学的概率;
(2)在教龄![]() 年以下,且经常使用信息技术教学的教师中任选
年以下,且经常使用信息技术教学的教师中任选![]() 人,其中恰有一人教龄在
人,其中恰有一人教龄在![]() 年以下的概率是多少?
年以下的概率是多少?