Question

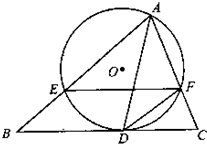
（2009•大连一模）选修4-1：几何证明选讲
如图，AD是△ABC的角平分线，经过点A、D的⊙D和BC切于D，且与AB、AC相交于E、F，连结DF．
（I）求证：EF∥BC；
（II）求证：DF²=AF•BE．

Answer 1

分析：（I）利用弦切角定理、角平分线的性质、同圆弧所对的圆周角相等、平分线的性质定理即可证明；
（II）利用弦切角定理可得∠BAD=∠BDE．于是∠BDE=∠FAD，利用圆的内接四边形的性质可得∠BED=∠DFA，可得△BED∽△DFA．及DE=DF，即可得出结论．

解答：证明：（I）∵⊙O切BC于D，
∴∠CAD=∠CDF，
∵AD是△ABC的角平分线，
∴∠BAD=∠DAC，
又∠BAD=∠EFD，
∴∠EFD=∠CDF，
∴EF∥BC．
（II）连接DE，
∵⊙O切BC于D，∴∠BAD=∠BDE．
由（I）可得∠BDE=∠FAD，
又∵⊙O内接四边形AEDF，∴∠BED=∠DFA，
∴△BED∽△DFA．
∴

DE

AF

=

BE

DF

．
又∵∠BAD=∠CDA，∴DE=DF，
∴DF²=AF•BE．

点评：熟练掌握弦切角定理、角平分线的性质、同圆弧所对的圆周角相等、平分线的性质定理、圆的内接四边形的性质、相似三角形的判定与性质定理是解题的关键．