��Ŀ����
��ƽ��ֱ������ϵxOy�У���֪����C1Ϊ������ �ľ����뵽��ֱ��
�ľ����뵽��ֱ��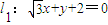 �ľ�����ȵĶ���P�Ĺ켣������C2��������C1������ԭ��O��˳ʱ�뷽����ת30°�γɵģ�
�ľ�����ȵĶ���P�Ĺ켣������C2��������C1������ԭ��O��˳ʱ�뷽����ת30°�γɵģ���1��������C1��������Ľ������꣬�Լ�����C2�ķ��̣�
��2��������M��m��0����m��2����ֱ��l2������C2��A��B���㣬��֪����C2�ϴ��ڲ�ͬ������C��D����ֱ��l2�Գƣ��ʣ��ҳ�|CD|�Ƿ�������ֵ�������ڣ��������ֵ���������ڣ���˵�����ɣ�
���𰸡���������1�����������ľ��빫ʽ�������ߵĶ����֪����C1Ϊ�����ߣ���������C1�ĶԳ��ᡢ���㡢�߿�֪��C2���ԣ�1��0��Ϊ���㣬��x=-1Ϊ�ߵ������ߣ��ó����ɣ�
��2����������C2�ϴ��ڲ�ͬ������C��D����ֱ��l2�Գƣ����ֱ��l2��б�ʿɵ�ֱ��CD�ķ��̣��������߷�����������������ϵ���Ĺ�ϵ���ɵó��ҳ�|CD|��ͨ����Ԫ���ö��κ����ĵ����Լ��ɵó���
����⣺��1����P��x��y���������⣬��֪����C1Ϊ�����ߣ�������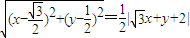 ��
��
����������C1�ķ���Ϊ��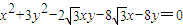 ��
��
��x=0����y=0��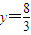 ��
��
��y=0����x=0�� ��
��
������C1��������Ľ�������Ϊ��0��0���� ��
��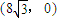 ��
��
�������֪������C1Ϊ�����ߣ����������ߴ�ֱ��ֱ��Ϊ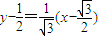 ����Ϊ
����Ϊ ��
��
��֪�˶Գ����ԭ�㣬��б��Ϊ30°��
�ֽ��� ��
��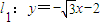 �ľ���Ϊ
�ľ���Ϊ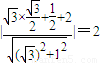 ��
��
��C2���ԣ�1��0��Ϊ���㣬��x=-1Ϊ�ߵ������ߣ��䷽��Ϊ��y2=4x��
��2����C��x1��y1����D��x2��y2����
������ֱ֪��l2��б��k�����Ҳ�Ϊ�㣬��ֱ��l2�ķ���Ϊy=k��x-m������ֱ��CD�ķ���Ϊ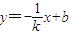 ��
��
��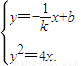 ��y2+4ky-4kb=0��
��y2+4ky-4kb=0��
���=16k��k+b����0��
��y1+y2=-4k��y1•y2=-4kb��
����CD���е�ΪG��x3��y3������y3=-2k��x3=k��b+2k����
��G��x3��y3����ֱ��l2�ϣ�-2k=k��bk+2k2-m������ ��
��
���ڴ���٣���0��k2��m-2��
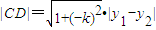 =
=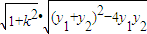 =
=
��t=k2����0��t��m-2��
���캯��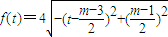 ��0��t��m-2��
��0��t��m-2��
����֪m��2����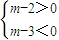 ����2��m��3ʱ��f��t�������ֵ�������ҳ�|CD|���������ֵ��
����2��m��3ʱ��f��t�������ֵ�������ҳ�|CD|���������ֵ��
��m��3ʱ��f��t�������ֵ2��m-1�������ҳ�|CD|�����ֵ2��m-1����
�������������������ߵĶ��弰�����ʡ�ֱ�����������ཻ����ת��ΪһԪ���η��̵ĸ���ϵ���Ĺ�ϵ���ҳ���ʽ����Ԫ�������κ����ĵ����ԡ��������۵�˼�뷽���ǽ���Ĺؼ���
��2����������C2�ϴ��ڲ�ͬ������C��D����ֱ��l2�Գƣ����ֱ��l2��б�ʿɵ�ֱ��CD�ķ��̣��������߷�����������������ϵ���Ĺ�ϵ���ɵó��ҳ�|CD|��ͨ����Ԫ���ö��κ����ĵ����Լ��ɵó���
����⣺��1����P��x��y���������⣬��֪����C1Ϊ�����ߣ�������
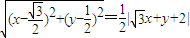 ��
������������C1�ķ���Ϊ��
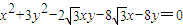 ��
����x=0����y=0��
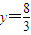 ��
����y=0����x=0��
 ��
��������C1��������Ľ�������Ϊ��0��0����
 ��
��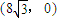 ��
���������֪������C1Ϊ�����ߣ����������ߴ�ֱ��ֱ��Ϊ
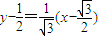 ����Ϊ
����Ϊ ��
����֪�˶Գ����ԭ�㣬��б��Ϊ30°��
�ֽ���
 ��
��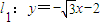 �ľ���Ϊ
�ľ���Ϊ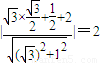 ��
����C2���ԣ�1��0��Ϊ���㣬��x=-1Ϊ�ߵ������ߣ��䷽��Ϊ��y2=4x��
��2����C��x1��y1����D��x2��y2����
������ֱ֪��l2��б��k�����Ҳ�Ϊ�㣬��ֱ��l2�ķ���Ϊy=k��x-m������ֱ��CD�ķ���Ϊ
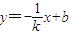 ��
����
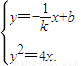 ��y2+4ky-4kb=0��
��y2+4ky-4kb=0�����=16k��k+b����0��
��y1+y2=-4k��y1•y2=-4kb��
����CD���е�ΪG��x3��y3������y3=-2k��x3=k��b+2k����
��G��x3��y3����ֱ��l2�ϣ�-2k=k��bk+2k2-m������
 ��
�����ڴ���٣���0��k2��m-2��
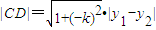 =
=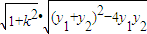 =
=
��t=k2����0��t��m-2��
���캯��
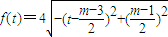 ��0��t��m-2��
��0��t��m-2������֪m��2����
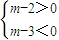 ����2��m��3ʱ��f��t�������ֵ�������ҳ�|CD|���������ֵ��
����2��m��3ʱ��f��t�������ֵ�������ҳ�|CD|���������ֵ����m��3ʱ��f��t�������ֵ2��m-1�������ҳ�|CD|�����ֵ2��m-1����
�������������������ߵĶ��弰�����ʡ�ֱ�����������ཻ����ת��ΪһԪ���η��̵ĸ���ϵ���Ĺ�ϵ���ҳ���ʽ����Ԫ�������κ����ĵ����ԡ��������۵�˼�뷽���ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ������ϵxOy�У���Ǧ��Ͷ۽Ǧµ��ձ߷ֱ��뵥λԲ����A��B���㣮����A�ĺ�������
��ͼ����ƽ��ֱ������ϵxOy�У���Ǧ��Ͷ۽Ǧµ��ձ߷ֱ��뵥λԲ����A��B���㣮����A�ĺ�������