题目内容
18.二维空间中,正方形的一维测度(周长)l=4a(其中a为正方形的边长),二维测度(面积)S=a2;三维空间中,正方体的二维测度(表面积)S=6a2(其中a为正方形的边长),三维测度(体积)V=a3;应用合情推理,若四维空间中,“超立方”的三维测度V=4a3,则其四维测度W=$\frac{{a}^{4}}{2}$.分析 根据所给的示例及类比推理的规则得出高维的测度的导数是底一维的测度,从而得到W′=V,从而求出所求.
解答 解:二维空间中,正方形的一维测度(周长)l=4a(其中a为正方形的边长),二维测度(面积)S=a2;
三维空间中,正方体的二维测度(表面积)S=6a2(其中a为正方形的边长),三维测度(体积)V=a3;
应用合情推理,若四维空间中,“超立方”的三维测度V=4a3,则其四维测度W=$\frac{{a}^{4}}{2}$,
故答案为:$\frac{{a}^{4}}{2}$.
点评 本题考查类比推理,解题的关键是理解类比的规律,解题的关键主要是通过所给的示例及类比推理的规则得出高维的测度的导数是低一维的测度,属于基础题.

练习册系列答案
相关题目
6.函数f(x)=3+xlnx的单调递减区间是( )
| A. | ($\frac{1}{e}$,e) | B. | (0,$\frac{1}{e}$) | C. | (-∞,$\frac{1}{e}$) | D. | ($\frac{1}{e}$,+∞) |
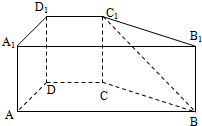 如图,已知直四棱柱ABCD-A1B1C1D1中,AA1=2,底面ABCD是直角梯形,A是直角,AB∥CD,AB=4,AD=2,DC=1,求异面直线BC1与DC所成角的余弦值.
如图,已知直四棱柱ABCD-A1B1C1D1中,AA1=2,底面ABCD是直角梯形,A是直角,AB∥CD,AB=4,AD=2,DC=1,求异面直线BC1与DC所成角的余弦值.