题目内容
【题目】如图,△ABC中,AB⊥BC,∠ACB=60°,D为AC中点,△ABD沿BD翻折过程中,直线AB与直线BC所成的最大角、最小角分别记为α1,β1,直线AD与直线BC所成最大角、最小角分别记为α2,β2,则有( )
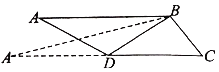
A.α1<α2,β1≤β2B.α1<α2,β1>β2
C.α1≥α2,β1≤β2D.α1≥α2,β1>β2
【答案】D
【解析】
翻折到180°时,AB,BC所成角最小,β1=30°,AD,BC所成角最小,β2=0°,翻折0°时,AB,BC所成角最大,可知α1=90°,翻折过程中,可知AD的投影可与BC垂直,从而AD,BC所成最大角α2=90°,推导出α1=90°,β1=30°,α2=90°,β2=0°.
翻折到180°时,AB,BC所成角最小,可知β1=30°,
![]() ,AD,BC所成角最小,β2=0°,
,AD,BC所成角最小,β2=0°,
翻折0°时,AB,BC所成角最大,可知α1=90°,
翻折过程中,可知AD的投影可与BC垂直,
所以AD,BC所成最大角α2=90°,
所以α1=90°,β1=30°,α2=90°,β2=0°.
故α1≥α2,β1>β2.
故选:D.

练习册系列答案
相关题目