题目内容
在数列{an}中，其前n项和Sn=4n+a，若数列{an}是等比数列，则常数a的值为______．
由Sn=4n+a，得a1=S1=4+a，
a1+a2=S2=16+a，所以a2=16+a-4-a=12，
a3=S3-S2=43+a-42-a=48．
因为数列{an}是等比数列，所以122=48（4+a），解得a=-1．
故答案为-1．
a1+a2=S2=16+a，所以a2=16+a-4-a=12，
a3=S3-S2=43+a-42-a=48．
因为数列{an}是等比数列，所以122=48（4+a），解得a=-1．
故答案为-1．
练习册系列答案
相关题目
___________.
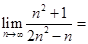