题目内容

已知抛物线C1：y2=4x与抛物线C2关于直线y=x对称，C1与C2交于M，N两点，则线段|MN|的长度为（　　）
A、4
B、4
2
C、8
D、8
2
分析：由抛物线C1：y2=4x与抛物线C2关于直线y=x对称知抛物线C2为x2=4y，解方程组
y2=4x
x2=4y
，得M（0，0），N（4，4），由此能求出线段|MN|的长度．
解答：解：由题设知抛物线C2为x2=4y，
解方程组
y2=4x
x2=4y
，得M（0，0），N（4，4），
∴|MN|=
16+16
=4
2
．
故选B．
点评：本题考查对称的性质与应用和两点间距离公式的应用，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
已知抛物线C1：y2=4mx（m＞0）的焦点为F2，其准线与x轴交于点F1，以F1，F2为焦点，离心率为
12
的椭圆C2与抛物线C1在x轴上方的一个交点为P．
（1）当m=1时，求椭圆的标准方程及其右准线的方程；
（2）用m表示P点的坐标；
（3）是否存在实数m，使得△PF1F2的边长是连续的自然数，若存在，求出这样的实数m；若不存在，请说明理由．
已知抛物线C1：y2=x+7，圆C2：x2+y2=5．
（1）求证抛物线与圆没有公共点；
（2）过点P（a，0）作与x轴不垂直的直线l交C1，C2依次为A、B、C、D，若|AB|=|CD|，求实数a的变化范围．
（2012•河北模拟）已知抛物线C1：y2=2px和圆C2：(x-
p
2
)2+y2=
p2
4
，其中p＞0，直线l经过C1的焦点，依次交C1，C2于A，B，C，D四点，则
AB
•
CD
的值为
p2
4
p2
4
．
已知抛物线C1：y2=2px（p＞0）的焦点F以及椭圆C2：
y2
a2
+
y2
b2
=1，(a＞b＞0)的上、下焦点及左、右顶点均在圆O：x2+y2=1上．
（Ⅰ）求抛物线C1和椭圆C2的标准方程；
（Ⅱ）过点F的直线交抛物线C1于A、B两不同点，交y轴于点N，已知
NA
=λ1
AF
， 
NB
 =λ2
BF
，求证：λ1+λ2为定值．
（Ⅲ）直线l交椭圆C2于P、Q两不同点，P、Q在x轴的射影分别为P'、Q'，
OP
•
OQ
+
OP′
•
OQ′
 +1=0，若点S满足：
OS
= 
OP
 +
OQ
，证明：点S在椭圆C2上．
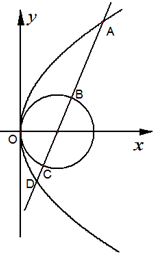精英家教网已知抛物线C1：y2=4x，圆C2：（x-1）2+y2=1，过抛物线焦点F的直线l交C1于A，D两点（点A在x轴上方），直线l交C2于B，C两点（点B在x轴上方）．
（Ⅰ）求|AB|•|CD|的值；
（Ⅱ）设直线OA、OB、OC、OD的斜率分别为m、n、p、q，且满足m+n+p+q=3
2
，并且|AB|，|BC|，|CD|成等差数列，求出所有满足条件的直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网