题目内容
【题目】已知函数![]() 与
与![]() 互为相反数,且
互为相反数,且![]() ,函数
,函数![]() 的定义域为
的定义域为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值域;
的值域;
(3)若函数![]() 的最大值为
的最大值为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)a=log32.(2)[﹣2,0].(3)λ![]() .
.
【解析】
(1)先求得![]() ,再根据f(a+2)=18计算a;
,再根据f(a+2)=18计算a;
(2)令t=2x,结合二次函数闭区间上最值的求解即可.
(3)讨论对称轴与区间[1,2]的关系得出h(t)的单调性,根据最大值为![]() 计算λ.
计算λ.
(1)由题意函数![]() 与
与![]() 互为相反数,∴
互为相反数,∴![]() ,
,
又∵f(a+2)=3a+2=18,∴3a=2,即a=log32.
(2)当![]() 时,由(1)可知
时,由(1)可知![]() ,
,
令t=2x,
由x∈[0,1]可得t∈[1,2],g(t)=t﹣t2在[1,2]上单调递减,
故当t=1时有最大值0,t=2时有最小值﹣2,
故值域[﹣2,0].
(3)∵函数![]() 的最大值为
的最大值为![]() ,由(2)可知:即为h(t)=﹣t2+λt,t∈[1,2]的最大值为
,由(2)可知:即为h(t)=﹣t2+λt,t∈[1,2]的最大值为![]() ,
,
①若![]() 2即λ≥4,则h(t)在[1,2]上单调递增,
2即λ≥4,则h(t)在[1,2]上单调递增,
∴h(2)=﹣4+2λ![]() ,解得λ
,解得λ![]() (舍).
(舍).
②若![]() 1即λ≤2时,则h(t)在[1,2]上单调递减,
1即λ≤2时,则h(t)在[1,2]上单调递减,
∴h(1)=﹣1+λ![]() ,解得λ
,解得λ![]() (舍).
(舍).
③若1![]() 2,即2<λ<4,则h(t)在[1,2]上先增后减,
2,即2<λ<4,则h(t)在[1,2]上先增后减,
∴h(![]() )
)![]() ,解得λ
,解得λ![]() (舍负).
(舍负).
综上,λ![]() .
.

 每日10分钟口算心算速算天天练系列答案
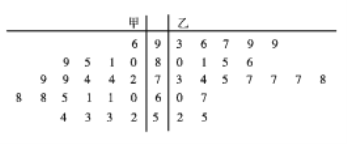
每日10分钟口算心算速算天天练系列答案【题目】为推行“新课堂”教学法,某老师分别用传统教学和“新课堂”两种不同的教学方式在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出如图所示的茎叶图,若成绩大于70分为“成绩优良”.
(1)由统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
(2)从甲、乙两班40个样本中,成绩在60分以下(不含60分)的学生中任意选取2人,求抽取的2人中恰有一人来自乙班的概率.
|
|
|
|
|
|
|
|
|
|
附:![]() ,(
,(![]() )
)