题目内容
【题目】直角坐标系
中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C的极坐标方程为：
，倾斜角为锐角的直线l过点
与单位圆
相切.
（1）求曲线C的直角坐标方程和直线l的参数方程；
（2）设直线l与曲线C交于A，B两点，求
的值.
【答案】（1）
，
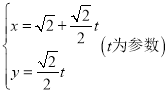；（2）
.
【解析】
(1)已知条件化简
,利用极坐标和直角坐标的互化公式即可得出结果,由倾斜角为锐角的直线l过点
与单位圆
相切,可得l的倾斜角为
,根据直线参数方程的定义即可得出结果.
(2)将直线参数方程和曲线
的普通方程联立,利用直线方程中参数的几何意义,可知
,借助韦达定理即可得出结果.
（1）
，
，
，
即曲线C的直角坐标方程为.
又依题意易得直线l的倾斜角为，所以直线l的参数方程为：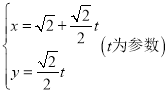
（2）将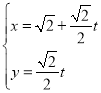
代入
中，整理得
，
所以
.
【题目】我国是全球最大的口罩生产国，在2020年3月份，我国每日口罩产量超一亿只，已基本满足国内人民的需求，但随着疫情在全球范围扩散，境外口罩需求量激增，世界卫生组织公开呼吁扩大口罩产能常见的口罩有
和
（分别阻挡不少于90.0%和95.0%的0.055到0.095微米的氯化钠颗粒）两种，某口罩厂两条独立的生产线分别生产和两种口罩，为保证质量对其进行多项检测并评分（满分100分），规定总分大于或等于85分为合格，小于85分为次品，现从流水线上随机抽取这两种口罩各100个进行检测并评分，结果如下：
总分 |
|
|
|
|
|
| 6 | 14 | 42 | 31 | 7 |
| 4 | 6 | 47 | 35 | 8 |
（1）试分别估计两种口罩的合格率；
（2）假设生产一个口罩，若质量合格，则盈利3元，若为次品则亏损1元；生产一个口罩，若质量合格，则盈利8元，若为次品则亏损2元，在（1）的前提下，
①设
为生产一个口罩和生产一个口罩所得利润的和，求随机变量的分布列和数学期望；
②求生产4个口罩所得的利润不少于8元的概率
【题目】为了引导居民合理用电，国家决定实行合理的阶梯电价，居民用电原则上以住宅为单位（一套住宅为一户）.
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用电范围（度） | （0,210] | （210,400] |
|
某市随机抽取10户同一个月的用电情况，得到统计表如下：
居民用电户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用电量（度） | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若规定第一阶梯电价每度0.5元，第二阶梯超出第一阶梯的部分每度0.6元，第三阶梯超出第二阶梯的部分每度0.8元，试计算A居民用电户用电410度时应电费多少元？
现要在这10户家庭中任意选取3户，求取到第二阶梯电量的户数的分布列与期望；
以表中抽到的10户作为样本估计全市的居民用电，现从全市中依次抽取10户，若抽到
户用电量为第一阶梯的可能性最大，求
的值.
【题目】某生物兴趣小组对冬季昼夜温差与反季节新品种大豆发芽数之间的关系进行研究，他们分别记录了
月
日至11月25日每天的昼夜温差与实验室每天100颗种子的发芽数，得到以下表格
日期 | 11月21日 | 11月22日 | 11月23日 | 11月24日 | 11月25日 |
温差( | 8 | 9 | 11 | 10 | 7 |
发芽数(颗) | 22 | 26 | 31 | 27 | 19 |
该兴趣小组确定的研究方案是：先从这5组数据中选取2组数据，然后用剩下的3组数据求线性回归方程，再用被选取的
组数据进行检验.
（1）求统计数据中发芽数的平均数与方差；
（2）若选取的是11月21日与11月25日的两组数据，请根据11月22 日至11月24 日的数据，求出发芽数
关于温差
的线性回归方程
，若由线性回归方程得到的估计数据与所选取的检验数据的误差不超过2，则认为得到的线性回归方程是可靠的，问得到的线性回归方程是否可靠？
附：线性回归方程 中斜率和截距最小二乘估法计算公式：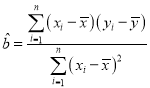
，
