题目内容
函数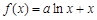 在区间
在区间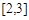 上单调递增,则实数a的取值范围为( ).
上单调递增,则实数a的取值范围为( ).
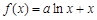 在区间
在区间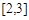 上单调递增,则实数a的取值范围为( ).
上单调递增,则实数a的取值范围为( ).A.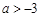 | B.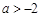 | C.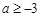 | D.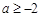 |
D
根据函数的导数与单调性的关系,f(x)=alnx+x在区间[2,3]上单调递增,只需f′(x)≥0在区间[2,3]上恒成立,考虑用分离参数法求解.
解:根据函数的导数与单调性的关系,f(x)=alnx+x在区间[2,3]上单调递增,只需f′(x)≥0在区间[2,3]上恒成立.
由导数的运算法则,f′(x)=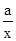 + 1≥0,移向得,
+ 1≥0,移向得,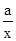 ≥ -1,a≥-x,,a只需大于等于-x的最大值即可,由-x≤-2,∴a≥-2
≥ -1,a≥-x,,a只需大于等于-x的最大值即可,由-x≤-2,∴a≥-2
故选D
解:根据函数的导数与单调性的关系,f(x)=alnx+x在区间[2,3]上单调递增,只需f′(x)≥0在区间[2,3]上恒成立.
由导数的运算法则,f′(x)=
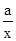 + 1≥0,移向得,
+ 1≥0,移向得,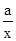 ≥ -1,a≥-x,,a只需大于等于-x的最大值即可,由-x≤-2,∴a≥-2
≥ -1,a≥-x,,a只需大于等于-x的最大值即可,由-x≤-2,∴a≥-2故选D

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
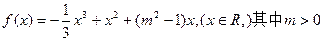
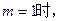 曲线
曲线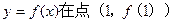 处的切线斜率
处的切线斜率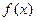 有三个互不相同的零点0,
有三个互不相同的零点0,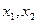 ,且
,且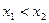 .若对任意的
.若对任意的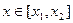 ,
,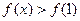 恒成立,求m的取值范围.
恒成立,求m的取值范围.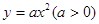 的两条切线互相垂直,则a为( )
的两条切线互相垂直,则a为( )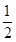
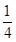
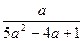 对称,求b的最小值.
对称,求b的最小值.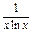 (x>0且x≠1).
(x>0且x≠1).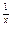 >xa对任意x∈(0,1)成立,求实数a的取值范围.
>xa对任意x∈(0,1)成立,求实数a的取值范围.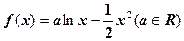 。(1)讨论函数
。(1)讨论函数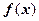 的单调性;(2)当
的单调性;(2)当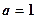 时,设
时,设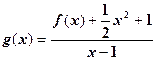 ,若
,若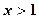 时,
时,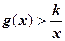 恒成立。求整数
恒成立。求整数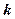 的最大值。
的最大值。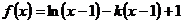
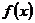 的单调区间和最大值;
的单调区间和最大值;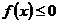 恒成立,求
恒成立,求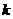 的取值范围;
的取值范围;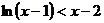 在
在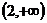 上恒成立;
上恒成立;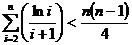
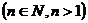
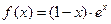 的单调递增区间是
的单调递增区间是  .
. 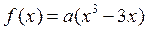 的递减区间为(-1,1),则a的取值范围是 .
的递减区间为(-1,1),则a的取值范围是 .