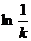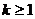题目内容
已知函数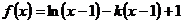
(1)求函数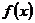 的单调区间和最大值;
的单调区间和最大值;
(2)若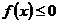 恒成立,求
恒成立,求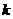 的取值范围;
的取值范围;
(3)证明:①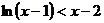 在
在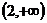 上恒成立;
上恒成立;
②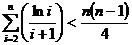
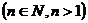
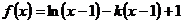
(1)求函数
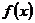 的单调区间和最大值;
的单调区间和最大值;(2)若
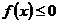 恒成立,求
恒成立,求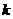 的取值范围;
的取值范围;(3)证明:①
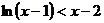 在
在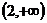 上恒成立;
上恒成立;②
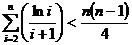
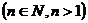
(1)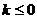 递增,
递增,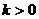
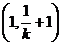 增,
增,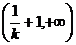 减,最大值
减,最大值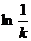
(2)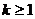
(3)略
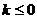 递增,
递增,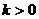
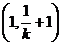 增,
增,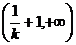 减,最大值
减,最大值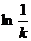
(2)
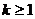
(3)略
略

练习册系列答案
相关题目
题目内容
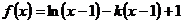
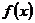 的单调区间和最大值;
的单调区间和最大值;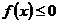 恒成立,求
恒成立,求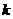 的取值范围;
的取值范围;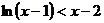 在
在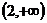 上恒成立;
上恒成立;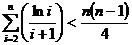
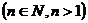
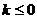 递增,
递增,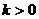
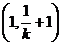 增,
增,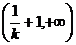 减,最大值
减,最大值