题目内容
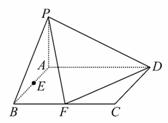
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
 (3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的平面角的余弦值.
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的平面角的余弦值.
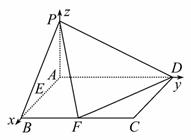 方法一:(1)∵PA⊥平面ABCD,∠BAD=90°,
方法一:(1)∵PA⊥平面ABCD,∠BAD=90°,
AB=1,AD=2,建立如图所示的空间直角坐标系Axyz,
则A(0,0,0),B(1,0,0),F(1,1,0),D(0,2,0).
不妨令P(0,0,t),∵![]() =(1,1,-t),
=(1,1,-t),![]() =(1,-1,0),
=(1,-1,0),
∴![]() ·
·![]() =1×1+1×(-1)+(-t)×0=0,
=1×1+1×(-1)+(-t)×0=0,
即PF⊥FD.
(2)存在.设平面PFD的一个法向量为n=(x,y,z),结合(1),
由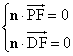 ,得
,得![]() ,
,
令z=1,解得:x=y=![]() .∴n=(
.∴n=(![]() ,
,![]() ,1).
,1).
设G点坐标为(0,0,m),E(![]() ,0,0),则
,0,0),则![]() =(-
=(-![]() ,0,m),
,0,m),
要使EG∥平面PFD,![]() 只需
只需![]() ·n=0,即(-
·n=0,即(-![]() )×
)×![]() +0×
+0×![]() +m×1=m-
+m×1=m-![]() =0,
=0,
得m=![]() t,从而满足AG=
t,从而满足AG=![]() AP的点G即为所求.
AP的点G即为所求.
(3)∵AB⊥平面PAD,∴![]() 是平面PAD的法向量,易得
是平面PAD的法向量,易得![]() =(1,0,0),
=(1,0,0),
又∵PA⊥平面ABCD,∴∠PBA是PB与平面ABCD所成的角,
得∠PBA=45°,PA=1,结合(2)得平面PFD的法向量为n=(![]() ,
,![]() ,1),
,1),
∴cos〈![]() ,n〉=
,n〉=![]() =
=![]() =
=![]() ,
,
由题意知二面角A-PD-F为锐二面角.
故所求二面角A-PD-F的平面角的余弦值为![]() .
.
方法二:(1)连接AF,则AF=![]() ,DF=
,DF=![]() ,
,![]()
又AD=2,∴DF2+AF2=AD2,∴DF⊥AF,
又PA⊥平面ABCD,∴DF⊥PA,又PA∩AF=A,
∴DF⊥平面PAF,又∵PF⊂平面PAF,∴DF⊥PF.
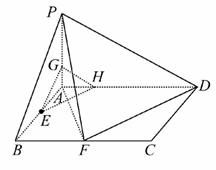 (2)过点E作EH∥DF交AD于点H,则EH∥平面PFD,且有AH=
(2)过点E作EH∥DF交AD于点H,则EH∥平面PFD,且有AH=![]() AD,
AD,
再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=![]() AP,
AP,
∴平面EHG∥平面PFD,∴EG∥平面PFD.
从而满足AG=![]() AP的点G即为所求.
AP的点G即为所求.
(3)∵PA⊥平面ABCD,∴∠PBA是PB与平面ABCD所成的角,且∠PBA=45°,∴PA=AB=1,
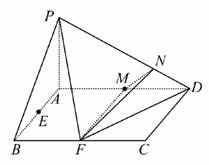 取AD的中点M,则FM⊥AD,FM⊥平面PAD,
取AD的中点M,则FM⊥AD,FM⊥平面PAD,
在平面PAD中,过M作MN⊥PD于N,连接FN,则PD⊥平面FMN,
则∠MNF即为二面角A—PD—F的平面角,
∵Rt△MND∽Rt△PAD,∴![]() =
=![]() ,
,
∵PA=1,MD=1,PD=![]() ,∴MN=
,∴MN=![]() ,
,
又∵∠FMN=90°,∴FN=![]() =
=![]() ,
,
∴cos∠MNF=![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ< (2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.