Question

【题目】已知椭圆 的两个焦点分别为 ， ，且经过点 .
（Ⅰ）求椭圆 的标准方程；
（Ⅱ） 的顶点都在椭圆 上，其中 关于原点对称，试问 能否为正三角形？并说明理由.

Answer 1

【答案】解：(Ⅰ)设椭圆 的标准方程为 ，
依题意得 ，
，
所以 ， ，
故椭圆 的标准方程为 .
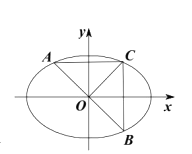
(Ⅱ)若 为正三角形，则 且 ，

显然直线 的斜率存在且不为0，
设 方程为 ，
则 的方程为 ，联立方程 ，
解得 ， ，
所以 ，
同理可得 .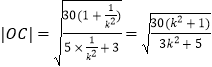
又 ，所以 ，
化简得 无实数解，
所以 不可能为正三角形
【解析】（Ⅰ）根据题目中所给的条件的特点，设出椭圆的标准方程并得到c，再由定义求得a，结合条件求得b，椭圆方程可求；
（Ⅱ）根据题意，直线AB的斜率存在且不为0，设AB方程为y=kx，写出直线OC的方程，分别联立直线方程与椭圆方程，求出A，C的坐标，得到|OC|与|OA|，代入条件得出k无实数解，说明△ABC不可能为正三角形．