题目内容
【题目】点M（x，y）与定点F（1，0）的距离和它到直线l：x=2的距离的比为 
，
（Ⅰ）求点M的轨迹．
（Ⅱ）是否存在点M到直线 
+y=1的距离最大？最大距离是多少？
【答案】解：（Ⅰ）由题意得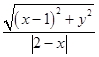 
= 
化简得 
=1
所以，点M的轨迹是长轴、短轴长分别为2 
，2的椭圆．
（Ⅱ）设直线m平行于直线l，m： 
+y=t，联立椭圆方程，消去x，可得（t﹣y）2=1﹣y2 ，
令关于y方程（t﹣y）2=1﹣y2的根的判别式为零解得t= 
．
当t=﹣ 时直线m与椭圆的交点到直线l的距离最远，d=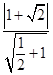 
= 
【解析】（Ⅰ）利用直接法，求出轨迹方程，即可求点M的轨迹．
（Ⅱ）设直线m平行于直线l，m： 
+y=t，联立椭圆方程，令关于y方程（t﹣y）2=1﹣y2的根的判别式为零解得t，即可得出结论．
【题目】某商场每天以每件100元的价格购入A商品若干件，并以每件200元的价格出售，若所购进的A商品前8小时没有售完，则商场对没卖出的A商品以每件60元的低价当天处理完毕（假定A商品当天能够处理完）．该商场统计了100天A商品在每天的前8小时的销售量，制成如表格．
前8小时的销售量t（单位：件） | 5 | 6 | 7 |
频 数 | 40 | 35 | 25 |
（1）若某天该商场共购入7件A商品，在前8个小时售出5件． 若这些产品被7名不同的顾客购买，现从这7名顾客中随机选3人进行回访，记X表示这3人中以每件200元的价格购买的人数，求X的分布列；
（2）将频率视为概率，要使商场每天购进A商品时所获得的平均利润最大，则每天应购进几件A商品，并说明理由．
【题目】天水市第一次联考后，某校对甲、乙两个文科班的数学考试成绩进行分析，
规定：大于或等于120分为优秀，120分以下为非优秀．统计成绩后，
得到如下的
列联表，且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
（1）请完成上面的列联表；
（2）根据列联表的数据，若按99.9%的可靠性要求，能否认为“成绩与班级有关系”；
（3）若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表：
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】近年来空气质量逐步恶化，雾霾天气现象增多，大气污染危害加重，大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关，在市第一人民医院随机对入院50人进行了问卷调查，得到如下的列联表：
患心肺疾病 | 不患心肺疾病 | 合计 | |||||||||
男 | 20 | 5 | 25 | ||||||||
女 | 10 | 15 | 25 | ||||||||
合计 | 30 | 20 | 50 | ||||||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | ||||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | ||||
（1）是否有99.5%的把握认为患心肺疾病与性别有关？说明你的理由；（2）已知在患心肺疾病的10位女性中，有3位又患有胃病，现在从患心肺疾病的10位女性中，选出3位进行其他方面的排查，其中患胃病的人数为
，求的分布列、数学期望.参考公式：
，其中
