Question

【题目】已知△ABC的顶点A（0，1），AB边上的中线CD所在的直线方程为2x﹣2y﹣1=0，AC边上的高BH所在直线的方程为y=0．
（1）求△ABC的顶点B、C的坐标；
（2）若圆M经过不同的三点A、B、P（m，0），且斜率为1的直线与圆M相切于点P，求圆M的方程．

Answer 1

【答案】
（1）解：AC边上的高BH所在直线的方程为y=0，所以直线AC的方程为：x=0，

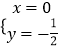又直线CD的方程为：2x﹣2y﹣1=0，联立得 解得 ，所以 ，

设B（b，0），则AB的中点 ，代入方程2x﹣2y﹣1=0，解得b=2，所以B（2，0）；

（2）解：由A（0，1），B（2，0）可得，圆M的弦AB的中垂线方程为4x﹣2y﹣3=0，

注意到BP也是圆M的弦，所以，圆心在直线 上，

设圆心M坐标为 ，

因为圆心M在直线4x﹣2y﹣3=0上，所以2m﹣2n+1=0①，

又因为斜率为1的直线与圆M相切于点P，所以kMP=﹣1，

即 ，整理得m﹣2n﹣2=0②，

由①②解得m=﹣3， ，

所以，圆心 ，半径 ，

则所求圆方程为 + = ，化简得x2+y2+x+5y﹣6=0．

【解析】（1）由AC边上的高BH所在直线的方程为y=0即x轴，得到AC边所在直线的方程为x=0即y轴，把x=0与2x﹣2y﹣1=0联立即可求出C的坐标，因为点B在x轴上，可设B的坐标为（b，0）利用中点坐标公式求出AB的中点D的坐标，把D的坐标代入到中线CD的方程中即可求出b的值，得到B的坐标；（2）根据A和B的坐标求出线段AB的垂直平分线方程，根据B和P的坐标求出线段BP的垂直平分线方程，设出圆心M的坐标，代入AB垂直平分线方程得到①，然后根据斜率为1的方程与圆相切，利用两直线垂直时斜率乘积为﹣1得到直线MP的斜率为﹣1，根据M和P的坐标表示出直线MP的斜率让其等于﹣1得到②，联立①②即可求出圆心M的坐标，然后利用两点间的距离公式求出线段MA的长度即为圆的半径，根据所求的圆心M和半径写出圆的方程即可．