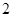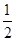题目内容
观察(x2)′=2x,(x4)′=4x3,(cosx)′=-sinx,由归纳推理可得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)=( )
| A.f(x) | B.-f(x) | C.g(x) | D.-g(x) |
D
由(x2)′=2x中,原函数为偶函数,导函数为奇函数;(x4)′=4x3中,原函数为偶函数,导函数为奇函数;(cosx)′=-sinx中,原函数为偶函数,导函数为奇函数;…我们可以推断,偶函数的导函数为奇函数.若定义在R上的函数f(x)满足f(-x)=f(x),则函数f(x)为偶函数,又∵g(x)为f(x)的导函数,则g(x)奇函数,
故g(-x)+g(x)=0,即g(-x)=-g(x),故选D
故g(-x)+g(x)=0,即g(-x)=-g(x),故选D

练习册系列答案
相关题目
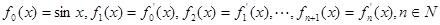 ,则
,则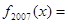 ( )
( )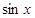
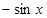
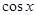
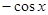
 (Ⅱ)
(Ⅱ)
 (Ⅳ)
(Ⅳ) .
. 在
在 处有极小值
处有极小值 ,
, 的值,并求出
的值,并求出 的单调区间.
的单调区间. 的方程
的方程 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围. ,若
,若 ,则
,则 ▲ ;
▲ ; 等于( )
等于( )



 的导数为_____________________;
的导数为_____________________;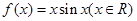 在
在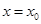 处取得极值,则
处取得极值,则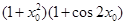 的值为( )
的值为( )