题目内容
【题目】已知![]() ,当点
,当点![]() 在
在![]() 的图象上运动时,点
的图象上运动时,点![]() 在函数
在函数![]() 的图象上运动(
的图象上运动(![]() ).
).
(Ⅰ)求![]() 和
和![]() 的表达式;
的表达式;
(Ⅱ)已知关于![]() 的方程
的方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,函数
,函数![]() 的值域为
的值域为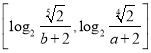 ,求实数
,求实数![]() 的值.
的值.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
试题分析:(Ⅰ)根据题意,联立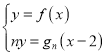 ,从而可得解.由
,从而可得解.由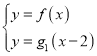 ,得
,得![]() ,从而可得
,从而可得![]() ,同理可求得
,同理可求得![]() ;(Ⅱ)由(Ⅰ)得
;(Ⅱ)由(Ⅰ)得![]() ,即
,即![]() ,分离参数得
,分离参数得![]() ,再由换元法求二次函数的最值,从而问题可得解;(Ⅲ)由(Ⅰ)、(Ⅱ)可求得函数
,再由换元法求二次函数的最值,从而问题可得解;(Ⅲ)由(Ⅰ)、(Ⅱ)可求得函数![]() 的解析式,并对函数
的解析式,并对函数![]() 的单调性进行判断,利用函数单调性求函数的最值,由题意,可建立关于
的单调性进行判断,利用函数单调性求函数的最值,由题意,可建立关于![]() 的方程组
的方程组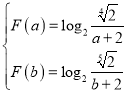 ,从而可得解.
,从而可得解.
试题解析:(Ⅰ)由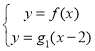 得,
得,![]()
![]() . …… 2分
. …… 2分
由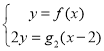 得,
得,![]()
![]() . …… 4分
. …… 4分
(Ⅱ)方程![]() 有实根
有实根![]() ,
,
分离![]() 得
得![]() . …… 6分
. …… 6分
设![]()
![]() …… 8分
…… 8分
(Ⅲ)![]() ,
,![]()
下面证明![]() 在
在![]() 上是减函数
上是减函数
任取![]() ,则
,则![]()
![]()
![]()
即![]() 在
在![]() 上递减,故在
上递减,故在![]() 在
在![]() 上递减 …… 10分
上递减 …… 10分
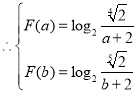 ,即
,即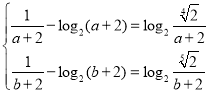 ,解得
,解得![]() ,
,
故![]() . …… 12分
. …… 12分

练习册系列答案
相关题目
【题目】为了普及环保知识增强环保意识,某校从理工类专业甲班抽取60人,从文史类乙班抽取50人参加环保知识测试.
(1)根据题目条件完成下面2×2列联表,并据此判断你是否有99%的把握认为环保知识与专业有关?
优秀 | 非优秀 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(2)为参加上级举办的环保知识竞赛,学校举办预选赛,预选赛答卷满分100分,优秀的同学得60分以上通过预选,非优秀的同学得80分以上通过预选,若每位同学得60分以上的概率为![]()
![]() ,得80分以上的概率为
,得80分以上的概率为![]() ,现已知甲班有3人参加预选赛,其中1人为优秀学生,若随机变量X表示甲班通过预选的人数,
,现已知甲班有3人参加预选赛,其中1人为优秀学生,若随机变量X表示甲班通过预选的人数,
求X的分布列及期望E(X).
附: ![]() , n=a+b+c+d
, n=a+b+c+d
P(K2>k0) | 0.100 | 0.050 | 0.025 | 0.010[ | 0.005 |
k0 | 2.706 | 3.84 | 5.02 | 6.635 | 7.879 |