Question

【题目】如图，已知二次函数y=x2+bx+c过点A（1，0），C（0，﹣3）

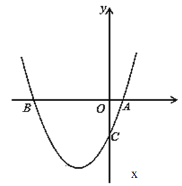
（1）求此二次函数的解析式；

（2）在抛物线上存在一点P使△ABP的面积为10，求点P的坐标．

Answer 1

【答案】（1）y=x2+2x﹣3（2）P（﹣4，5）（2，5）

【解析】

试题分析：（1）利用待定系数法把A（1，0），C（0，-3）代入二次函数y=x2+bx+c中，即可算出b、c的值，进而得到函数解析式是y=x2+2x-3；（2）首先求出A、B两点坐标，再算出AB的长，再设P（m，n），根据△ABP的面积为10可以计算出n的值，然后再利用二次函数解析式计算出m的值即可得到P点坐标

试题解析：（1）∵二次函数y=x2+bx+c过点A（1，0），C（0，﹣3），

∴，解得，

∴二次函数的解析式为y=x2+2x﹣3；

（2）∵当y=0时，x2+2x﹣3=0，解得：x1=﹣3，x2=1；

∴A（1，0），B（﹣3，0），∴AB=4，

设P（m，n），∵△ABP的面积为10，∴AB|n|=10，解得：n=±5，

当n=5时，m2+2m﹣3=5，解得：m=﹣4或2，∴P（﹣4，5）（2，5）；

当n=﹣5时，m2+2m﹣3=﹣5，方程无解，

故P（﹣4，5）（2，5）；