题目内容
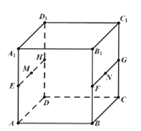
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.
求证:(1)PA∥平面EFG;
(2)DH⊥平面EFG.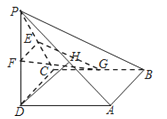
【答案】证明:(1)∵E、G分别是PC、BC的中点,
∴EG是△PBC的中位线,
∴EG∥PB,
又∵PB平面PAB,EG平面PAB,
∴EG∥平面PAB,
∵E、F分别是PC、PD的中点,
∴EF∥CD,
又∵底面ABCD为正方形,
∴CD∥AB,
∴EF∥AB,
又∵AB平面PAB,EF平面PAB,
∴EF∥平面PAB,
又EF∩EG=E,
∴平面EFG∥平面PAB,
∵PA平面PAB,
∴PA∥平面EFG.
(2)∵PD⊥AD,PD=AD,H为的中点,
∴DH⊥PA,
∵BA⊥平面PDA,DH平面PDA,
∴DH⊥AB,
∴DH⊥平面PAB,
∴DH⊥PB,
由(1)EF∥AB,EG∥PB,
∴DH⊥EG,DH⊥EF,
∴DH⊥平面EFG.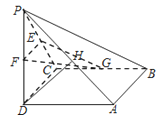
【解析】(1)根据面面平行的性质推出线面平行;
(2)由题意可证DH⊥PA,DH⊥AB,可证DH⊥平面PAB,从而证明DH⊥PB,由(1)EF∥AB,EG∥PB,从而证明DH⊥EG,DH⊥EF,即可证明DH⊥平面EFG.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握直线与平面垂直的性质(垂直于同一个平面的两条直线平行)的相关知识才是答题的关键.

【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
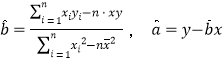 .
.