题目内容
18.已知函数f(x)=2sin2x+2$\sqrt{3}$sinxcosx+1.(1)求f(x)的最小正周期;
(2)求f(x)的单调递增区间;
(3)画出y=f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象;
(4)求f(x)在[0,$\frac{π}{2}$]的最小值及取得最小值时x的值.
分析 (1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=2+2sin(2x-$\frac{π}{6}$),由三角函数的周期性及其求法即可得解.
(2)由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z可解得f(x)的单调递增区间.
(3)由五点作图法即可画出y=f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象.
(4)由x∈[0,$\frac{π}{2}$],可求2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],从而可求f(x)在[0,$\frac{π}{2}$]的最小值及取得最小值时x的值.
解答 解:(1)∵f(x)=2sin2x+2$\sqrt{3}$sinxcosx+1=1-cos2x+$\sqrt{3}$sin2x+1=2+2sin(2x-$\frac{π}{6}$),
∴f(x)的最小正周期T=$\frac{2π}{2}$=π.
(2)∵2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z可解得:kπ$-\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,k∈Z,
∴f(x)的单调递增区间是:[kπ$-\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z,
(3)画出y=f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象如下: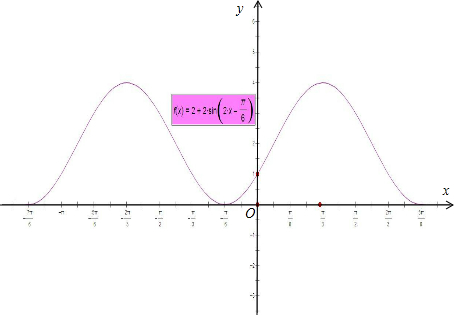
(4)∵x∈[0,$\frac{π}{2}$],
∴2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],f(x)=2+2sin(2x-$\frac{π}{6}$)∈[0,4],
∴当x=-$\frac{π}{6}$,或$\frac{5π}{6}$时,f(x)在[0,$\frac{π}{2}$]的最小值为0.
点评 本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的单调性,五点作图法画函数的图象等知识的综合应用,属于基本知识的考查.

| A. | -$\frac{5}{2}$ | B. | $\frac{3}{2}$ | C. | -4 | D. | -2 |
| A. | y=-$\frac{1}{x}$ | B. | y=ln|x| | ||
| C. | y=sinx | D. | y=$\left\{\begin{array}{l}{x+1,x>0}\\{x-1,x<0}\end{array}\right.$ |

| A. | k≤2013? | B. | k≤2014? | C. | k≥2013? | D. | k≥2014? |
 如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC,AB=BC=CA=$\frac{1}{2}A{A_1}$=1,∠A1AB=120°,D、E分别是BC、A1C1的中点.
如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC,AB=BC=CA=$\frac{1}{2}A{A_1}$=1,∠A1AB=120°,D、E分别是BC、A1C1的中点.

 {,
{,