题目内容
8. 如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC,AB=BC=CA=$\frac{1}{2}A{A_1}$=1,∠A1AB=120°,D、E分别是BC、A1C1的中点.
如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC,AB=BC=CA=$\frac{1}{2}A{A_1}$=1,∠A1AB=120°,D、E分别是BC、A1C1的中点.(Ⅰ)试在棱AB上找一点F,使DE∥平面A1CF;
(Ⅱ)在(Ⅰ)的条件下,求多面体BCF-A1B1C1的体积.
分析 (Ⅰ)F是AB的中点,连接DF,利用三角形的中位线定理与平行四边形的判定定理可得:四边形A1FDE是平行四边形,可得DE∥A1F,再利用线面平行的判定定理可得:DE∥平面A1CF.
(II)连接AB1,在△AA1B1中,∠AA1B1=60°,A1A=2,A1B1=1,根据余弦定理可得AB1,利用勾股定理的逆定理可得:A1B1⊥AB1,再利用等边三角形的性质、面面垂直的性质可得:AB1是三棱柱ABC-A1B1C1的高.利用多面体BCF-A1B1C1的体积V=${V_{三棱柱ABC-{A_1}{B_1}{C_1}}}$-V三棱锥$_{C-{A_1}AF}$即可得出.
解答 解:(Ⅰ)F是AB的中点,证明如下: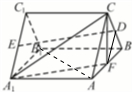
连接DF,
∵D、E分别是BC、A1C1的中点,
∴DF$\stackrel{∥}{=}$$\frac{1}{2}$AC,又AC$\stackrel{∥}{=}$A1C1,且A1E=$\frac{1}{2}$A1C1,
则DF$\stackrel{∥}{=}$A1E,
∴四边形A1FDE是平行四边形,
∴DE∥A1F,又A1F?平面A1CF,DE?平面A1CF,
∴DE∥平面A1CF.
(Ⅱ)连接AB1,在△AA1B1中,∠AA1B1=60°,A1A=2,A1B1=1,
根据余弦定理,$A{B_1}=\sqrt{{2^2}+{1^2}-2×2×1×cos{{60}°}}=\sqrt{3}$,
则$AB_1^2+{A_1}B_1^2={A_1}{A^2}$,
∴A1B1⊥AB1,
由(Ⅰ)知,F是AB的中点,则CF⊥AB,面ABB1A1⊥面ABC,
∴AB1⊥底面ABC,即AB1是三棱柱ABC-A1B1C1的高.
∴${V_{三棱柱ABC-{A_1}{B_1}{C_1}}}$=$\frac{{\sqrt{3}}}{4}×\sqrt{3}=\frac{3}{4}$,
V三棱锥$_{C-{A_1}AF}$=$\frac{1}{3}×\frac{1}{2}×2×\frac{1}{2}×sin{120°}×\frac{{\sqrt{3}}}{2}=\frac{1}{8}$,
∴多面体BCF-A1B1C1的体积V=${V_{三棱柱ABC-{A_1}{B_1}{C_1}}}$-V三棱锥$_{C-{A_1}AF}$=$\frac{3}{4}-\frac{1}{8}$=$\frac{5}{8}$.
点评 本题考查了三角形的中位线定理、平行四边形的判定与性质定理、线面平行的判定定理、余弦定理、勾股定理的逆定理、等边三角形的性质、面面垂直的性质、三棱柱与三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

| A. | 310 | B. | 212 | C. | 180 | D. | 121 |
| A. | [-5,5] | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | [-$\frac{1}{3}$,0)∪(0,$\frac{1}{3}$] | D. | [-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$] |
| A. | 135 | B. | 172 | C. | 189 | D. | 216 |
 设平行于y轴的直线分别与函数y1=log2x及y2=log2x+2的图象交于B,C两点,点A(m,n)位于函数y2的图象上,若△ABC为正三角形,则m•2n=( )
设平行于y轴的直线分别与函数y1=log2x及y2=log2x+2的图象交于B,C两点,点A(m,n)位于函数y2的图象上,若△ABC为正三角形,则m•2n=( )| A. | 8$\sqrt{3}$ | B. | 12 | C. | 12$\sqrt{3}$ | D. | 15 |
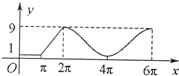
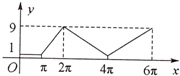
 如图所示的图形是由一个半径为2的圆和两个半径为1的半圆组成,它们的圆心分别为O,O1,O2.动点P从A点出发沿着圆弧按A→O→B→C→A→D→B的路线运动(其中A,O1,O,O2,B五点共线),记点P运动的路程为x,设y=|O1P|2,y与x的函数关系为y=f(x),则y=f(x)的大致图象是( )
如图所示的图形是由一个半径为2的圆和两个半径为1的半圆组成,它们的圆心分别为O,O1,O2.动点P从A点出发沿着圆弧按A→O→B→C→A→D→B的路线运动(其中A,O1,O,O2,B五点共线),记点P运动的路程为x,设y=|O1P|2,y与x的函数关系为y=f(x),则y=f(x)的大致图象是( )