题目内容
9.已知函数f(x)=alnx+$\frac{2(1-x)}{1+x}$(a∈R)定义域为(0,1),则f(x)的图象不可能是( )| A. | 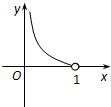 | B. |  | C. |  {, {, | D. |  |
分析 已知函数f(x),在函数式中含有参数,所以本题在定义域内对参数的讨论是本题的重点,可以对参数a分以下几种情况进行讨论①a=0②a<0③a>0根据不同的情况进行具体分析.
解答 解:f(x)=alnx+$\frac{2(1-x)}{1+x}$(a∈R),定义域为(0,1),下面把参数分以下三种情况进行讨论:
(1)当a=0 函数f(x)=$\frac{2(1-x)}{1+x}$>0.故A符合,
(2)当a<0 用单调性来进行讨论,由于函数y=lnx在定义域(0,1)内为增函数,则y=alnx为减函数,
同时y=$\frac{2(1-x)}{1+x}$=$\frac{4}{1+x}$-2也为减函数,所以函数f(x)为减函数,故A符合,
(3)当a>0 利用函数的导数来讨论,则f′(x)=$\frac{a}{x}$+$\frac{-4}{(1+x)^{2}}$=$\frac{a{x}^{2}+(2a-4)x+4}{x(1+x)^{2}}$,
令f′(x)=0 即ax2+(2a-4)x+a=0,
则△=16-16a下面再分三种情况讨论,
①当a=1,f′(x)=$\frac{{x}^{2}-2x+1}{x(1+x)^{2}}$=$\frac{(x-1)^{2}}{x(1+x)^{2}}$>0 则函数f(x)为增函数,故B符合.
②当1>a>0时ax2+(2a-4)x+a=0存在两根x1=$\frac{2-a+2\sqrt{1-a}}{a}$,x2=$\frac{2-a-2\sqrt{1-a}}{a}$,由于1>a>0则 得到1>x1>0,x2>1,
当x1>x>0函数图象为增函数 当x1<x<1时为减函数,故C符合,
③当a>1时 f′(x)>0恒成立,故B符合,
通过以上讨论,排除得到答案应D,
故选:D.
点评 本题利用的知识点较多,通过函数的值,函数的单调性,以及导数进行分类讨论难度较大.分类讨论是解决本题的关键,属于难题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 310 | B. | 212 | C. | 180 | D. | 121 |

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | x1>x2 | B. | x1+x2=0 | C. | x1<x2 | D. | x12<x22 |
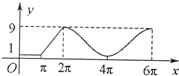
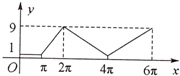
 如图所示的图形是由一个半径为2的圆和两个半径为1的半圆组成,它们的圆心分别为O,O1,O2.动点P从A点出发沿着圆弧按A→O→B→C→A→D→B的路线运动(其中A,O1,O,O2,B五点共线),记点P运动的路程为x,设y=|O1P|2,y与x的函数关系为y=f(x),则y=f(x)的大致图象是( )
如图所示的图形是由一个半径为2的圆和两个半径为1的半圆组成,它们的圆心分别为O,O1,O2.动点P从A点出发沿着圆弧按A→O→B→C→A→D→B的路线运动(其中A,O1,O,O2,B五点共线),记点P运动的路程为x,设y=|O1P|2,y与x的函数关系为y=f(x),则y=f(x)的大致图象是( )