题目内容
在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列
(Ⅰ)求d,an;
(Ⅱ)若d<0,求|a1|+|a2|+|a3|+…+|an|.
【命题意图】本题考查等差数列、等比数列的概念,等差数列通项公式、求和公式等基础知识,同时考查运算求解能力。
【答案解析】
(Ⅰ)由题意
5a3× a1=(2a2+2)2,
即
d2−3d−4=0.
故
d=−1或d=4.
所以
an=−n+11,nÎN*或an=4n+6,nÎN*
(Ⅱ)设数列{an}的前n项和为Sn.因为d<0,由(Ⅰ)得d=−1,an=−n+11.则
当n£11时,
|a1|+|a2|+|a3|+…+|an|=Sn=−![]() n2+
n2+![]() n
n
当n³12时,
|a1|+|a2|+|a3|+…+|an|=−Sn+2S11=![]() n2−
n2−![]() n+110
n+110
综上所述,
|a1|+|a2|+|a3|+…+|an|=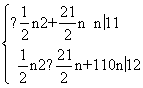

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目