题目内容
已知函数 (
( ).
).
(1)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)
 内角
内角 的对边长分别为
的对边长分别为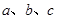 ,若
,若
 且
且 试求角B和角C.
试求角B和角C.
 (
( ).
).(1)求函数
 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; (2)

 内角
内角 的对边长分别为
的对边长分别为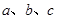 ,若
,若
 且
且 试求角B和角C.
试求角B和角C.(1)故函数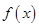 的最小正周期为
的最小正周期为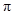 ;递增区间为
;递增区间为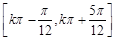 (
( Z )
Z )
(2)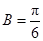 .
. 
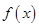 的最小正周期为
的最小正周期为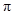 ;递增区间为
;递增区间为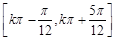 (
( Z )
Z ) (2)
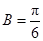 .
. 
本试题主要是考查了三角函数的化简和性质的运用 ,以及解三角形中正弦定理的边角转换的运用。
(1)因为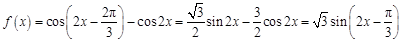 ,这样可知其性质。
,这样可知其性质。
(2)由第一问可知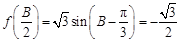 ,那么得到角B的值,然后再由正弦定理得:
,那么得到角B的值,然后再由正弦定理得:
得到sinC,,得到角C的值。
解:(Ⅰ)∵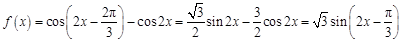 ,
,
∴故函数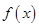 的最小正周期为
的最小正周期为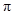 ;递增区间为
;递增区间为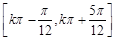 (
( Z )
Z )
(Ⅱ)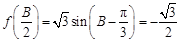 ,∴
,∴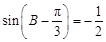 .
.
∵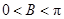 ,∴
,∴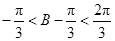 ,∴
,∴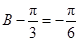 ,即
,即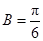 .由正弦定理得:
.由正弦定理得: ,∴
,∴ ,∵
,∵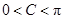 ,∴
,∴ 或
或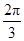 .
.
当 时,
时,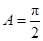 ;当
;当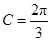 时,
时, .(不合题意,舍)
.(不合题意,舍)
所以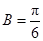 .
. 
(1)因为
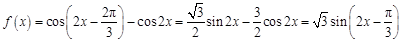 ,这样可知其性质。
,这样可知其性质。(2)由第一问可知
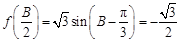 ,那么得到角B的值,然后再由正弦定理得:
,那么得到角B的值,然后再由正弦定理得:
得到sinC,,得到角C的值。
解:(Ⅰ)∵
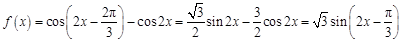 ,
,∴故函数
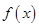 的最小正周期为
的最小正周期为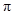 ;递增区间为
;递增区间为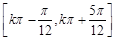 (
( Z )
Z )(Ⅱ)
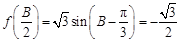 ,∴
,∴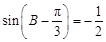 .
.∵
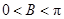 ,∴
,∴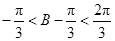 ,∴
,∴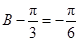 ,即
,即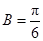 .由正弦定理得:
.由正弦定理得: ,∴
,∴ ,∵
,∵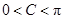 ,∴
,∴ 或
或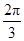 .
.当
 时,
时,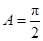 ;当
;当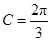 时,
时, .(不合题意,舍)
.(不合题意,舍)所以
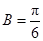 .
. 

练习册系列答案
相关题目
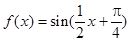 ,求函数在区间
,求函数在区间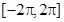 上的单调增区间;
上的单调增区间;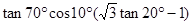 .
.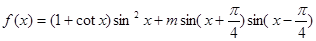 .
. 在区间
在区间 上的取值范围;
上的取值范围; 时,
时, ,求m的值.
,求m的值.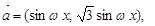
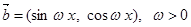
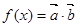 ,
,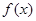 的最小正周期为
的最小正周期为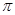 .
. 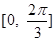 上的取值范围.
上的取值范围.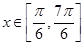 时,函数
时,函数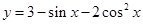 的最小值是_______,最大值是________。
的最小值是_______,最大值是________。
 的最小正周期和最小值;
的最小正周期和最小值; 的内角
的内角 对边分别为
对边分别为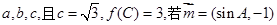 与
与 垂直,求
垂直,求 的值.
的值.
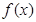 的最小正周期和值域;
的最小正周期和值域; ,且
,且 ,求
,求 的值.
的值.
 ,试在下坐标系中画出
,试在下坐标系中画出 图像的示意图,并据此回答:不等式
图像的示意图,并据此回答:不等式 的解集.
的解集.
 ,最小值为
,最小值为 ,求a,b 的值.
,求a,b 的值.