题目内容
定义域为R的函数f(x)=a-2bcosx(b>0)的最大值为 ,最小值为
,最小值为 ,求a,b 的值.
,求a,b 的值.
 ,最小值为
,最小值为 ,求a,b 的值.
,求a,b 的值.解:∵b>0
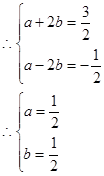 ……………8分
……………8分
……………12分
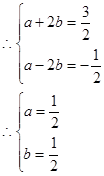 ……………8分
……………8分……………12分
本试题主要是考查而来三角函数的最值的运用,先分析定义域为R的函数f(x)=a-2bcosx(b>0)的最大值为 ,最小值为
,最小值为 ,用参数a,b表示出来,然后解得。
,用参数a,b表示出来,然后解得。
 ,最小值为
,最小值为 ,用参数a,b表示出来,然后解得。
,用参数a,b表示出来,然后解得。
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 在一个周期内的图象如图,求函数的解析式
在一个周期内的图象如图,求函数的解析式
 (
( ).
). 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 
 内角
内角 的对边长分别为
的对边长分别为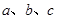 ,若
,若
 且
且 试求角B和角C.
试求角B和角C. 在
在 上的递增区间为 .
上的递增区间为 .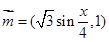 ,
, ,
,
 ,求
,求 的值;
的值; 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围.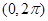 内,使
内,使 成立的
成立的 的取值范围为( )
的取值范围为( )



 的最小正周期为
的最小正周期为 




 ,
, ,那么
,那么 = ( )
= ( ) 



 的图象的一条对称轴是( )
的图象的一条对称轴是( )


