题目内容
【题目】已知函数f(x)= ![]() x2﹣2ax+lnx(a∈R),x∈(1,+∞).
x2﹣2ax+lnx(a∈R),x∈(1,+∞).
(1)若函数f(x)有且只有一个极值点,求实数a的取值范围;
(2)对于函数f(x)、f1(x)、f2(x),若对于区间D上的任意一个x,都有f1(x)<f(x)<f2(x),则称函数f(x)是函数f1(x)、f2(x)在区间D上的一个“分界函数”.已知f1(x)=(1﹣a2)lnx,f2(x)=(1﹣a)x2 , 问是否存在实数a,使得f(x)是函数f1(x)、f2(x)在区间(1,+∞)上的一个“分界函数”?若存在,求实数a的取值范围;若不存在,说明理由.
【答案】
(1)解:f′(x)= ![]() ,x∈(1,+∞),
,x∈(1,+∞),
令g(x)=x2﹣2ax+1,由题意得:g(x)在[1,+∞)有且只有1个零点,
∴g(1)<0,解得:a>1
(2)解:若f(x)是函数f1(x)、f2(x)在区间(1,+∞)上的一个“分界函数”,
则x∈(1,+∞)时,f(x)﹣(1﹣a)x2<0恒成立且f(x)﹣(1﹣a2)lnx>0恒成立,
令h(x)=f(x)﹣(1﹣a)x2=(a﹣ ![]() )x2﹣2ax+lnx,
)x2﹣2ax+lnx,
则h′(x)= ![]() ,
,
①2a﹣1≤0即a≤ ![]() 时,当x∈(1,+∞)时,h′(x)<0,h(x)递减,且h(1)=﹣
时,当x∈(1,+∞)时,h′(x)<0,h(x)递减,且h(1)=﹣ ![]() ﹣a,
﹣a,
∴h(1)≤0,解得:﹣ ![]() ≤a≤
≤a≤ ![]() ;
;
②2a﹣1>0即a> ![]() 时,y=(a﹣
时,y=(a﹣ ![]() )x2﹣2ax的图象开口向上,
)x2﹣2ax的图象开口向上,
存在x0>1,使得(a﹣ ![]() )
) ![]() ﹣2ax0>0,
﹣2ax0>0,
从而h(x0)>0,h(x)<0在(1,+∞)不恒成立,
令m(x)=f(x)﹣(1﹣a2)lnx= ![]() x2﹣2ax+a2lnx,
x2﹣2ax+a2lnx,
则m′(x)= ![]() ≥0,m(x)在(1,+∞)递增,
≥0,m(x)在(1,+∞)递增,
由f(x)﹣(1﹣a2)lnx>0恒成立,得:m(1)≥0,解得:a≤ ![]() ,
,
综上,a∈[﹣ ![]() ,
, ![]() ]时,f(x)是函数f1(x)、f2(x)在区间(1,+∞)上的一个“分界函数”.
]时,f(x)是函数f1(x)、f2(x)在区间(1,+∞)上的一个“分界函数”.
【解析】(1)求出函数的导数,根据f(x)有且只有一个极值点,得到x2﹣2ax+1<0恒成立,求出a的范围即可;(2)根据“分界函数”的定义,只需x∈(1,+∞)时,f(x)﹣(1﹣a)x2<0恒成立且f(x)﹣(1﹣a2)lnx>0恒成立,判断函数的单调性,求出a的范围即可.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.
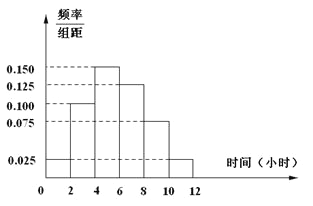
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |

