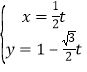Question

【题目】等差数列{an}的前n项和为Sn ， 且a1=1，S7=28，记bn=[lgan]，其中[x]表示不超过x的最大整数，如[0.9]=0，[lg99]=1，则数列{bn}的前1000项和为 ．

Answer 1

【答案】1893
【解析】解：Sn为等差数列{an}的前n项和，且a1=1，S7=28，7a4=28．
可得a4=4，则公差d=1．
an=n，
bn=[lgn]，则b1=[lg1]=0，b2=b3=…=b9=0，b10=b11=b12=…=b99=1．
b100=b101=b102=b103=…=b999=2，b1000=3．
数列{bn}的前1000项和为：9×0+90×1+900×2+3=1893．
所以答案是：1893．
【考点精析】掌握等差数列的前n项和公式是解答本题的根本，需要知道前n项和公式：．