题目内容
1．若f（1-2x）=$\frac{1-{x}^{2}}{{x}^{2}}$（x≠0），那么f（$\frac{1}{2}$）=（ ）| A． | 1 | B． | 3 | C． | 15 | D． | 30 |
分析 令1-2x=$\frac{1}{2}$，求出满足条件的x值，代入f（1-2x）=$\frac{1-{x}^{2}}{{x}^{2}}$（x≠0），可得f（$\frac{1}{2}$）的值．
解答 解：令1-2x=$\frac{1}{2}$，
则x=$\frac{1}{4}$，
∵f（1-2x）=$\frac{1-{x}^{2}}{{x}^{2}}$（x≠0），
∴f（$\frac{1}{2}$）=$\frac{1-{（\frac{1}{4}）}^{2}}{{（\frac{1}{4}）}^{2}}$=15，
故选：C
点评 本题考查的知识点是函数的值，难度不大，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
6．已知函数f（x）=2cos（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，其中（$\frac{2}{3}$，y1）与（$\frac{20}{3}$，y2）分别为函数f（x）图象的一个最高点和最低点，则函数（x）的一个单调增区间为（ ）
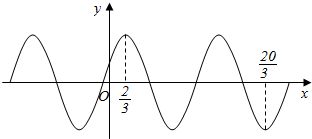
| A． | （-$\frac{16}{3}$，-$\frac{10}{3}$） | B． | （-$\frac{10}{3}$，0） | C． | （0，$\frac{4}{3}$） | D． | （$\frac{14}{3}$，$\frac{20}{3}$） |