题目内容
已知 =(2asin2x,a),
=(2asin2x,a), =(-1,2
=(-1,2 sinxcosx+1),O为坐标原点,a≠0,设f(x)=
sinxcosx+1),O为坐标原点,a≠0,设f(x)= ·
· +b,b>a。
+b,b>a。
(1)若a>0,写出函数y=f(x)的单调递增区间;
(2)若函数y=f(x)的定义域为[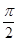 ,π],值域为[2,5],求实数a与b的值。
,π],值域为[2,5],求实数a与b的值。
 =(2asin2x,a),
=(2asin2x,a), =(-1,2
=(-1,2 sinxcosx+1),O为坐标原点,a≠0,设f(x)=
sinxcosx+1),O为坐标原点,a≠0,设f(x)= ·
· +b,b>a。
+b,b>a。(1)若a>0,写出函数y=f(x)的单调递增区间;
(2)若函数y=f(x)的定义域为[
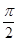 ,π],值域为[2,5],求实数a与b的值。
,π],值域为[2,5],求实数a与b的值。(1)f(x)=-2asin2x+2asinxcosx+a+b=2asin+b, 2分
∵a>0,
∴由2kπ-≤2x+≤2kπ+得,
kπ-≤x≤kπ+,k∈Z. 5分
∴函数y=f(x)的单调递增区间是[kπ-,kπ+](k∈Z) 6分
(2)x∈[,π]时,2x+∈[,], 8分
sin∈[-1,] 10分
当a>0时,f(x)∈[-2a+b,a+b]
∴,得, 12分
当a<0时,f(x)∈[a+b,-2a+b]
∴,得 14分
综上知,或 16分
∵a>0,
∴由2kπ-≤2x+≤2kπ+得,
kπ-≤x≤kπ+,k∈Z. 5分
∴函数y=f(x)的单调递增区间是[kπ-,kπ+](k∈Z) 6分
(2)x∈[,π]时,2x+∈[,], 8分
sin∈[-1,] 10分
当a>0时,f(x)∈[-2a+b,a+b]
∴,得, 12分
当a<0时,f(x)∈[a+b,-2a+b]
∴,得 14分
综上知,或 16分
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,
 时,求函数
时,求函数 的最小值.
的最小值. ,不等式
,不等式 都成立,求实数
都成立,求实数 的范围.
的范围. sin(3x—
sin(3x— ) 的定义域是__________,值域是________,周期是________,振幅是________,初相是_________.
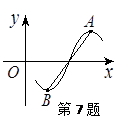
) 的定义域是__________,值域是________,周期是________,振幅是________,初相是_________.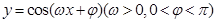 为奇函数,该函数的部分图像如右图所示,
为奇函数,该函数的部分图像如右图所示,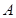 、
、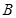 分别为最高点与最低点,且
分别为最高点与最低点,且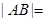
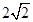 ,则该函数图象的一条对称轴为( )
,则该函数图象的一条对称轴为( )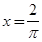
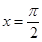
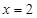
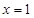
 ,
, ,其中
,其中 设函数
设函数 .
. 的最小正周期为
的最小正周期为 ,求函数
,求函数 ,求
,求 的值。
的值。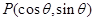 在直线
在直线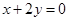 上,则
上,则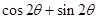 =( )
=( )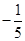
 ,则函数
,则函数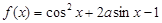 的最大值为_________.
的最大值为_________. 的周期为( )
的周期为( ) 



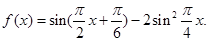
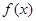 的最小正周期;
的最小正周期;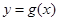 的图像与函数
的图像与函数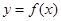 的图像关于原点对称,求
的图像关于原点对称,求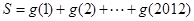 的值。
的值。