题目内容
函数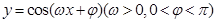 为奇函数,该函数的部分图像如右图所示,
为奇函数,该函数的部分图像如右图所示,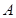 、
、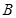 分别为最高点与最低点,且
分别为最高点与最低点,且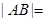
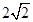 ,则该函数图象的一条对称轴为( )
,则该函数图象的一条对称轴为( )
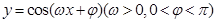 为奇函数,该函数的部分图像如右图所示,
为奇函数,该函数的部分图像如右图所示,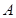 、
、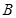 分别为最高点与最低点,且
分别为最高点与最低点,且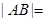
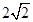 ,则该函数图象的一条对称轴为( )
,则该函数图象的一条对称轴为( )A.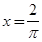 | B.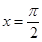 | C.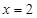 | D.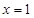 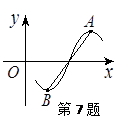 |
D
解:
解:函数y=cos(ωx+φ)(ω>0,0<φ<π)为奇函数,所以φ=π/2,该函数的部分图象如图所表示,A、B分别为最高点与最低点,并且两点间的距离为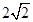 ,所以(
,所以(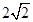 )2=22+(T/2)2,
)2=22+(T/2)2,
所以T=4,ω=π/2,所以函数的表达式为:y=-sinπ/2x,显然x=1是它的一条对称轴方程.
故选D
解:函数y=cos(ωx+φ)(ω>0,0<φ<π)为奇函数,所以φ=π/2,该函数的部分图象如图所表示,A、B分别为最高点与最低点,并且两点间的距离为
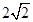 ,所以(
,所以(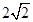 )2=22+(T/2)2,
)2=22+(T/2)2,所以T=4,ω=π/2,所以函数的表达式为:y=-sinπ/2x,显然x=1是它的一条对称轴方程.
故选D

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
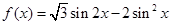 .
.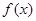 的最大值;
的最大值;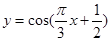 的图象作怎样的变换可以得到函数
的图象作怎样的变换可以得到函数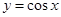 的图象?
的图象? =(2asin2x,a),
=(2asin2x,a), =(-1,2
=(-1,2 sinxcosx+1),O为坐标原点,a≠0,设f(x)=
sinxcosx+1),O为坐标原点,a≠0,设f(x)=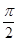 ,π],值域为[2,5],求实数a与b的值。
,π],值域为[2,5],求实数a与b的值。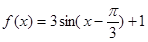 ,在下列四个命题中:
,在下列四个命题中: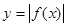 的最小正周期是
的最小正周期是 ;
;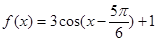 ;
;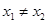 ,且
,且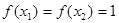 ,则
,则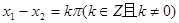 ;
; ,都有
,都有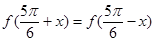 成立;
成立;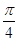 )cos(
)cos(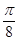
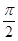
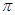
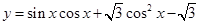 的图象的一条对称轴是( )
的图象的一条对称轴是( )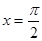
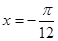
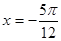
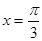
 。
。 ,则
,则 的最大值为
的最大值为