题目内容
在R上定义运算 ,若不等式
,若不等式 成立,则实数a的取值范围是( ).
成立,则实数a的取值范围是( ).
A.{a| } } | B.{a| } } |
C.{a| } } | D.{a| } } |
C
解析试题分析:由题知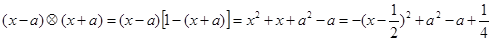
∴不等式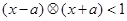 对任意实数x都成立转化为
对任意实数x都成立转化为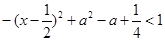 对任意实数x都成立,
对任意实数x都成立,
即 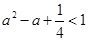 恒成立,解可得
恒成立,解可得 .故选A.
.故选A.
考点:本题考查了在新定义下对函数恒成立问题的应用.关于新定义型的题,关键是理解定义,并会用定义来解题.

练习册系列答案
相关题目
(5分)(2011•广东)函数f(x)=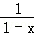 +lg(1+x)的定义域是( )
+lg(1+x)的定义域是( )
| A.(﹣∞,﹣1) | B.(1,+∞) | C.(﹣1,1)∪(1,+∞) | D.(﹣∞,+∞) |
对任意实数 ,
, 定义运算“⊙”:
定义运算“⊙”: 设
设 ,若函数
,若函数 的图象与
的图象与 轴恰有三个交点,则
轴恰有三个交点,则 的取值范围是( )
的取值范围是( )
A.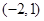 | B. |
C. | D.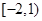 |
设定义域为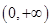 的单调函数
的单调函数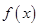 ,对任意的
,对任意的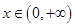 ,都有
,都有 ,若
,若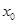 是方程
是方程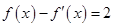 的一个解,则
的一个解,则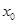 可能存在的区间是( )
可能存在的区间是( )
A.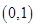 | B.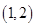 | C. | D.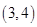 |
已知函数f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+m(m为常数),则f(-1)的值为( )
| A.-3 | B.-1 | C.1 | D.3 |
已知定义域为R的函数f(x)满足:f(4)=-3,且对任意x∈R总有f′(x)<3,则不等式f(x)<3x-15的解集为( )
| A.(-∞,4) |
| B.(-∞,-4) |
| C.(-∞,-4)∪(4,+∞) |
| D.(4,+∞) |
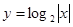

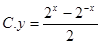
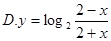
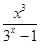 的图象大致是( )
的图象大致是( )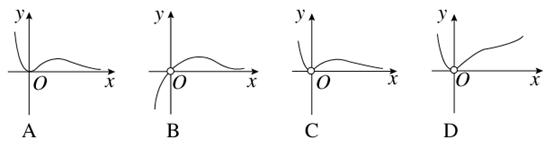
 (a≠0)在同一坐标系中的图象可能是( )
(a≠0)在同一坐标系中的图象可能是( )