题目内容
对任意实数 ,
, 定义运算“⊙”:
定义运算“⊙”: 设
设 ,若函数
,若函数 的图象与
的图象与 轴恰有三个交点,则
轴恰有三个交点,则 的取值范围是( )
的取值范围是( )
A.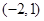 | B. |
C. | D.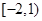 |
D
解析试题分析:∵ ,
,
∵函数 的图象与
的图象与 轴恰有三个交点,∴
轴恰有三个交点,∴ 的图像与
的图像与 的图像有三个交点,
的图像有三个交点,
∴ 的图像如图所示,
的图像如图所示, 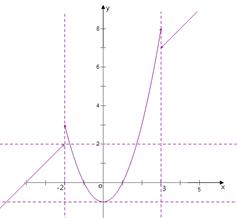
根据图像得: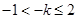 ,∴
,∴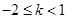 .
.
考点:函数图像.

练习册系列答案
相关题目
(5分)(2011•福建)若关于x的方程x2+mx+1=0有两个不相等的实数根,则实数m的取值范围是( )
| A.(﹣1,1) | B.(﹣2,2) | C.(﹣∞,﹣2)∪(2,+∞) | D.(﹣∞,﹣1)∪(1,+∞) |
在R上定义运算 ,若不等式
,若不等式 成立,则实数a的取值范围是( ).
成立,则实数a的取值范围是( ).
A.{a| } } | B.{a| } } |
C.{a| } } | D.{a| } } |
若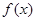 是偶函数,且当
是偶函数,且当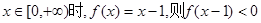 的解集是 ( )
的解集是 ( )
A. | B. | C. | D.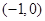 |
如果函数 在
在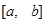 上的最大值和最小值分别为
上的最大值和最小值分别为 、
、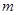 ,那么
,那么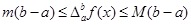 .根据这一结论求出
.根据这一结论求出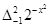 的取值范围( ).
的取值范围( ).
A.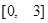 | B.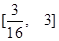  | C. | D.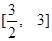 |
若函数y=ax与y=-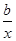 在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上( )
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上( )
| A.单调递增 | B.单调递减 |
| C.先增后减 | D.先减后增 |
函数f(x)=(x-3)ex的单调递增区间是( )
| A.(-∞,2) | B.(0,3) | C.(1,4) | D.(2,+∞) |
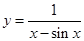 的一段大致图象是( )
的一段大致图象是( )