Question

【题目】设函数f（x）=sin（ ﹣ ）﹣2cos2 +1． （Ⅰ）求f（x）的最小正周期；
（Ⅱ）若函数y=g（x）与y=f（x）的图象关于直线x=1对称，求当x∈[0， ]时y=g（x）的最大值．

Answer 1

【答案】解：（Ⅰ）化简可得 x = sin（ ），
∴f（x）的最小正周期为 ；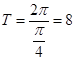
（Ⅱ）在y=g（x）的图象上任取一点（x，g（x）），
则它关于x=1的对称点（2﹣x，g（x））在y=f（x）的图象上，
∴g（x）=f（2﹣x）= sin[ （2﹣x）﹣ ]
= sin（ ﹣ x﹣ ）= cos（ x+ ）
当 时， ，
∴y=g（x）在区间 上的最大值为
【解析】（Ⅰ）化简可得f（x）= sin（ ），由周期公式可得；（Ⅱ）在y=g（x）的图象上任取一点（x，g（x）），则它关于x=1的对称点（2﹣x，g（x））在y=f（x）的图象上，可得g（x）=f（2﹣x）= cos（ x+ ），由 结合余弦函数的单调性可得．