题目内容
3.已知函数f(x)=3sin(ωx-$\frac{π}{6}$)(ω>0)和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同,若x∈[0,$\frac{π}{2}$],则f(x)的取值范围是( )| A. | [-3,3] | B. | [-$\frac{3}{2}$,$\frac{3}{2}$] | C. | [-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$] | D. | [-$\frac{3}{2}$,3] |
分析 先根据函数f(x)=3sin(ωx-$\frac{π}{6}$)和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同确定ω的值,再由x的范围确定ωx-$\frac{π}{6}$的范围,最后根据正弦函数的图象和性质可得到答案
解答 解:由题意可得ω=2,∵x∈[0,$\frac{π}{2}$],∴ωx-$\frac{π}{6}$=2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
由三角函数图象知:
f(x)的最小值为3sin(-$\frac{π}{6}$)=-$\frac{3}{2}$,最大值为3sin$\frac{π}{2}$=3,
所以f(x)的取值范围是[-$\frac{3}{2}$,3],
故选:D
点评 本题考查三角函数的图象与性质,考查了数形结合的数学思想,属于基础题

练习册系列答案
相关题目
13.函数f(x)=$\left\{\begin{array}{l}{\sqrt{x}-1,x≥0}\\{2cosx-1,-2π≤x<0}\end{array}\right.$的所有零点的和等于( )
| A. | 1-2π | B. | 1-$\frac{3π}{2}$ | C. | 1-π | D. | 1-$\frac{π}{2}$ |
11.设函数f(x)=x•lnx2,g(x)=$\left\{\begin{array}{l}{{e}^{x}-{e}^{-x},x>0}\\{{e}^{-x}-{e}^{x},x<0}\end{array}\right.$则下列命题正确的是( )
| A. | f(x)是奇函数,g(x)是奇函数 | B. | f(x)是偶函数,g(x)是奇函数 | ||
| C. | f(x)是奇函数,g(x)是偶函数 | D. | f(x)是偶函数,g(x)是偶函数 |
12.若实数x,y满足不等式组$\left\{\begin{array}{l}x+3y-3≤0\\ x-y+1≥0\\ y≥-1\end{array}\right.$则z=2|x|+y的取值范围是( )
| A. | [-1,3] | B. | [1,11] | C. | [1,3] | D. | [-1,11] |
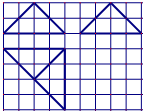 如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的表面积为8+12$\sqrt{2}$.
如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的表面积为8+12$\sqrt{2}$.