题目内容
7.若sinα$\sqrt{1-co{s}^{2}α}$+cosα$\sqrt{1-si{n}^{2}α}$=-1,则α的取值范围是[2kπ+π,2kπ+$\frac{3}{2}$π],k∈Z.分析 利用同角三角函数基本关系的运用化简函数后,通过对α所在象限讨论,化简求解即可.
解答 解:sinα$\sqrt{1-co{s}^{2}α}$+cosα$\sqrt{1-si{n}^{2}α}$=-1,
化为:sinα|sinα|+cosα|cosα|=-1,①
当α∈[2kπ,2kπ+$\frac{π}{2}$],k∈Z时,①不成立;
当α∈(2kπ+$\frac{π}{2}$,2kπ+π),k∈Z时,①不成立;
当α∈[2kπ+π,2kπ+$\frac{3}{2}$π],k∈Z时,①成立;
当α∈(2kπ+$\frac{3}{2}$π,2kπ+2π),k∈Z时,①不成立;
故α的取值范围是:[2kπ+π,2kπ+$\frac{3}{2}$π],k∈Z.
故答案为:[2kπ+π,2kπ+$\frac{3}{2}$π],k∈Z.
点评 本题主要考查了同角三角函数基本关系的运用,考查了分类讨论思想,属于基础题.

练习册系列答案
相关题目
3.已知命题p:对?x∈R,x2-x-1≥0恒成立.命题q:?x∈R是2x-1≤0成立.则下列命题中为真命题的是( )
| A. | (?p)∧q | B. | (?p)∧(?q) | C. | p∧(?q) | D. | p∧q |
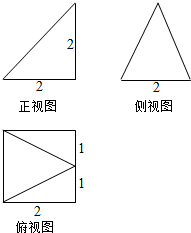 如图是一个几何体的三视图,根据图中所给的数据,求这个几何体的表面积和体积.
如图是一个几何体的三视图,根据图中所给的数据,求这个几何体的表面积和体积.