题目内容
知椭圆 的两焦点
的两焦点 、
、 ,离心率为
,离心率为 ,直线
,直线 :
: 与椭圆
与椭圆 交于
交于 两点,点
两点,点 在
在 轴上的射影为点
轴上的射影为点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)求直线 的方程,使
的方程,使 的面积最大,并求出这个最大值.
的面积最大,并求出这个最大值.
(1)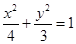 (2)直线
(2)直线 的方程为:
的方程为: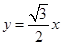 ,
, 的面积的最大值为
的面积的最大值为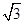
解析试题分析:(1)利用椭圆的基本性质求解
(2)利用弦长公式及基本不等式求解
试题解析:(1)设椭圆方程为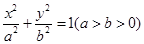 ,则
,则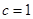
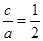 ,
,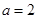 ,
,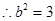
所以,所求椭圆方程为: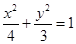 .
.
(2)由 得:
得: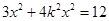 ,
,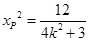
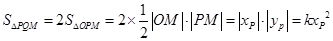
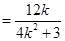
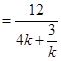
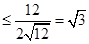
当且仅当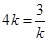 即
即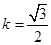 时取等号,
时取等号,
此时,直线 的方程为:
的方程为: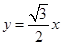 ,
, 的面积的最大值为
的面积的最大值为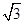 .
.
考点:直线与椭圆的有关知识、函数求最值的方法,数形结合的思想

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的离心率为,左焦点为F(-1,0),
的离心率为,左焦点为F(-1,0), ,求直线L的方程;
,求直线L的方程;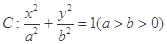 的离心率为
的离心率为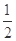 ,以原点
,以原点 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切。
相切。 的标准方程;
的标准方程;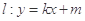 与椭圆
与椭圆 、
、 两点,且
两点,且 ,试判断
,试判断 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由. 的短半轴长为
的短半轴长为 ,动点
,动点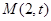
 在直线
在直线 (
( 为半焦距)上.
为半焦距)上. 为直径且被直线
为直径且被直线 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;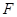 是椭圆的右焦点,过点
是椭圆的右焦点,过点 ,
, 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.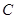 的中心在原点,右焦点为
的中心在原点,右焦点为 ,渐近线方程为
,渐近线方程为 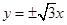 .
.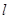 :
: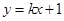 与双曲线
与双曲线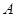 、
、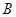 两点,问:当
两点,问:当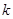 为何值时,以
为何值时,以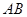 为直径的圆过原点;
为直径的圆过原点; 的由顶点为A,右焦点为F,直线
的由顶点为A,右焦点为F,直线 与x轴交于点B且与直线
与x轴交于点B且与直线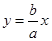 交于点C,点O为坐标原点,
交于点C,点O为坐标原点, ,过点F的直线
,过点F的直线 与椭圆交于不同的两点M,N.
与椭圆交于不同的两点M,N.
 的面积的最大值.
的面积的最大值. 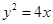 .
.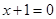 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;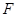 ,若过
,若过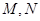 两点,若
两点,若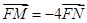 ,求直线
,求直线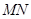 的斜率;
的斜率;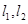 ,抛物线与
,抛物线与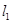 交于点
交于点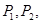 与
与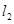 交于点
交于点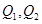 .
.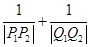 为一常数.
为一常数. 的离心率为
的离心率为 ,以椭圆的左顶点T为圆心作圆T:
,以椭圆的左顶点T为圆心作圆T: 设圆T与椭圆C交于点M、N.
设圆T与椭圆C交于点M、N.
 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程; 轴交于点R,S,O为坐标原点. 试问;是否存在使
轴交于点R,S,O为坐标原点. 试问;是否存在使 最大的点P,若存在求出P点的坐标,若不存在说明理由.
最大的点P,若存在求出P点的坐标,若不存在说明理由.