题目内容
如图;.已知椭圆C: 的离心率为
的离心率为 ,以椭圆的左顶点T为圆心作圆T:
,以椭圆的左顶点T为圆心作圆T: 设圆T与椭圆C交于点M、N.
设圆T与椭圆C交于点M、N.
(1)求椭圆C的方程;
(2)求 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与 轴交于点R,S,O为坐标原点. 试问;是否存在使
轴交于点R,S,O为坐标原点. 试问;是否存在使 最大的点P,若存在求出P点的坐标,若不存在说明理由.
最大的点P,若存在求出P点的坐标,若不存在说明理由.
(1) ;(2)
;(2) ;(3)存在
;(3)存在
解析试题分析:(1)椭圆C: 的离心率为
的离心率为


由椭圆的左顶点为 ,所以
,所以
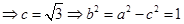 可得椭圆的标准方程
可得椭圆的标准方程 ;
;
(2)点M与点N关于 轴对称,设
轴对称,设 ,
,
 ,再根据
,再根据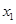 的取值范围求出
的取值范围求出 的范围.
的范围.
(3)假设存在点 使
使 取最大值,因为
取最大值,因为 =
=
利用点 分别是直线
分别是直线 与
与 轴的交点,把
轴的交点,把 表示成
表示成 的函数,进而求出其取最大值
的函数,进而求出其取最大值 的值,确定点
的值,确定点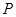 的坐标.
的坐标.
试题解析:
解:(1)由题意知 解之得;
解之得;  ,由
,由 得b=1,
得b=1,
故椭圆C方程为 ;.3分
;.3分
(2)点M与点N关于 轴对称,设
轴对称,设 , 不妨 设
, 不妨 设 , 由于点M在椭圆C上,
, 由于点M在椭圆C上,
 ,
,
由已知

 ,..6分由于
,..6分由于 故当
故当 时,
时, 取得最小值为
取得最小值为 ,
,
当 时
时 ,故
,故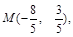 又点M在圆T上,代入圆的方程得
又点M在圆T上,代入圆的方程得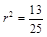 ,故圆T的方程为:
,故圆T的方程为: ;..8分
;..8分
(3)假设存在满足条件的点P,设 ,则直线MP的方程为:
,则直线MP的方程为: 令
令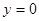 ,得
,得 ,同理
,同理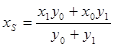 ,
,
故 ;..10分
;..10分
又点M与点P在椭圆上,故 ,
,
得 ,
, 为定值,.12分
为定值,.12分
 =
= =
=
 =
= ,
,
由P为椭圆上的一点, 要使
要使 最大,只要
最大,只要 最大,而
最大,而 的最大值为1,故满足条件的P点存在其坐标为
的最大值为1,故满足条件的P点存在其坐标为 ...14分
...14分
考点:1、椭圆的标准方程和圆的标准方程;2、直线与椭圆的位置关系;3、向量的数量积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在双曲线
在双曲线 上,且双曲线的一条渐近线的方程是
上,且双曲线的一条渐近线的方程是 .
. 的方程;
的方程;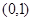 且斜率为
且斜率为 的直线
的直线 与双曲线
与双曲线 两个不同点,若以线段
两个不同点,若以线段 为直径的圆经过坐标原点,求实数
为直径的圆经过坐标原点,求实数 的两焦点
的两焦点 、
、 ,离心率为
,离心率为 ,直线
,直线 :
: 与椭圆
与椭圆 两点,点
两点,点 在
在 轴上的射影为点
轴上的射影为点 .
.
 的面积最大,并求出这个最大值.
的面积最大,并求出这个最大值. 的右焦点为
的右焦点为 ,点
,点 在椭圆上.
在椭圆上.
 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过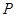 ,
,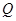 两点,问:△
两点,问:△ 的周长是否为定值?如果是,求出定值;如果不是,说明理由.
的周长是否为定值?如果是,求出定值;如果不是,说明理由. (a>0,b>0)的一个焦点坐标为(
(a>0,b>0)的一个焦点坐标为( ,0),离心率
,0),离心率 , A、B是双曲线上的两点,AB的中点M(1,2).
, A、B是双曲线上的两点,AB的中点M(1,2). =1(a>b>0,a、b为常数),动圆C1:x2+y2=
=1(a>b>0,a、b为常数),动圆C1:x2+y2= ,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: 为定值.
为定值. ,0)与定直线l1∶x=
,0)与定直线l1∶x= 的距离之比为常数
的距离之比为常数 .
. ·
· 的最小值,并求此时圆T的方程.
的最小值,并求此时圆T的方程. +y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.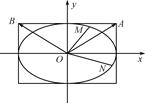
 =m
=m +n
+n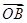 ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程; =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.