题目内容
已知椭圆 的由顶点为A,右焦点为F,直线
的由顶点为A,右焦点为F,直线 与x轴交于点B且与直线
与x轴交于点B且与直线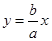 交于点C,点O为坐标原点,
交于点C,点O为坐标原点, ,过点F的直线
,过点F的直线 与椭圆交于不同的两点M,N.
与椭圆交于不同的两点M,N.
(1)求椭圆的方程;
(2)求 的面积的最大值.
的面积的最大值.
(1) ;(2)
;(2)
解析试题分析:(1)由直线 与x轴交于点B且与直线
与x轴交于点B且与直线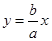 交于点C,
交于点C,  .即可得到关于
.即可得到关于 的两个方程.从而得到结论.
的两个方程.从而得到结论.
(2)首先考虑直线MN垂直于x轴的情况,求出 的面积.由(1)得到的方程联立直线方程,消去y得到一个关于x的方程,由韦达定理写出两个等式.由弦长公式即点到直线的距离公式,即可求出
的面积.由(1)得到的方程联立直线方程,消去y得到一个关于x的方程,由韦达定理写出两个等式.由弦长公式即点到直线的距离公式,即可求出 的面积的.再利用最值的求法,即可的结论.
的面积的.再利用最值的求法,即可的结论.
试题解析:(1) 因为 ,
,  ,则
,则 且
且 ,得
,得 则
则
椭圆方程为:
(2) ①当直线 与x轴不垂直时,设直线
与x轴不垂直时,设直线 ,
,
则 消去
消去 得
得 ,
,
所以 
记 为
为 到
到 的距离,则
的距离,则 ,
, 所以
所以 =
=

② 当 轴时,
轴时, ,所以
,所以 的面积的最大值为
的面积的最大值为
考点:1.待定系数法求椭圆的方程.2.韦达定理.3.弦长公式.4.点到直线的距离公式.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 到两个定点
到两个定点 、
、 的距离之和为
的距离之和为 ,线段
,线段 的长为
的长为 .
.
 的方程;
的方程; 与轨迹
与轨迹 两点,且点
两点,且点 的垂直平分线为
的垂直平分线为 .
. 的面积的最大值;
的面积的最大值; 、
、 关于直线
关于直线 ,|BC|=2|AC|.
,|BC|=2|AC|.
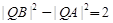 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由. 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: 为定值.
为定值. 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点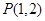 、
、 、
、 均在抛物线上.
均在抛物线上.
 与
与 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求 的值及直线
的值及直线 的斜率.
的斜率. 的两焦点
的两焦点 、
、 ,离心率为
,离心率为 ,直线
,直线 :
: 与椭圆
与椭圆 两点,点
两点,点 在
在 轴上的射影为点
轴上的射影为点 .
.
 的面积最大,并求出这个最大值.
的面积最大,并求出这个最大值. 是椭圆E:
是椭圆E: 的两个焦点,抛物线
的两个焦点,抛物线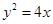 的焦点为椭圆E的一个焦点,直线y=
的焦点为椭圆E的一个焦点,直线y= 上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
 的动直线
的动直线 交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由. 的右焦点为
的右焦点为 ,点
,点 在椭圆上.
在椭圆上.
 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过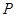 ,
,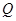 两点,问:△
两点,问:△ 的周长是否为定值?如果是,求出定值;如果不是,说明理由.
的周长是否为定值?如果是,求出定值;如果不是,说明理由. =1(a>b>0,a、b为常数),动圆C1:x2+y2=
=1(a>b>0,a、b为常数),动圆C1:x2+y2= ,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: 为定值.
为定值. 上任意一点
上任意一点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,且
,且 .
. 、
、 是曲线
是曲线 和
和 的倾斜角分别为
的倾斜角分别为 和
和 ,当
,当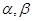 变化且
变化且 为定值
为定值 时,证明直线
时,证明直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.