题目内容
17.在矩形ABCD,AB=2,AD=1,边DC上(包含点D、C)的动点P与CB延长线上(包含点B)的动点Q满足|$\overline{DP}$|=|$\overline{BQ}$|,则向量$\overline{PA}$与向量$\overline{PQ}$的数量积$\overline{PA}$•$\overline{PQ}$的最小值为$\frac{3}{4}$.分析 以A为坐标原点,AB所在直线为x轴,建立直角坐标系,设P(x,1),则Q(2,-x)(0≤x≤2),求得向量$\overline{PA}$•$\overline{PQ}$,再由二次函数的最值求法,即可得到最小值.
解答 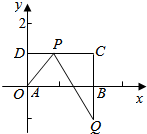 解:以A为坐标原点,AB所在直线为x轴,建立直角坐标系,
解:以A为坐标原点,AB所在直线为x轴,建立直角坐标系,
设P(x,1),则Q(2,-x)(0≤x≤2),
$\overrightarrow{PA}$=(-x,-1),$\overrightarrow{PQ}$=(2-x,-x-1),
即有$\overline{PA}$•$\overline{PQ}$=-x(2-x)+x+1=x2-x+1
=(x-$\frac{1}{2}$)2+$\frac{3}{4}$,
当x=$\frac{1}{2}$∈[0,2]时,取得最小值$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查向量的数量积的坐标表示,同时考查二次函数的最值的求法,考查运算能力,属于中档题.

练习册系列答案
相关题目